В данной статье основное внимание акцентируется на применении современных информационных технологий и математических знаний при решении научно-исследовательских в области физической культуры и спорта с учетом ведущей репрезентативной сенсорной системы студентов. В результате проведенного исследования выявлено сокращение времени, затрачиваемого на технические математические расчеты, которое позволяет увеличить число практических задач, решаемых на одном аудиторном занятии. Это дает возможность выработать устойчивые умения и навыки при решении задач данного типа и повысить качество подготовки магистрантов.
Ключевые слова: современные информационные технологии, физическая культура и спорт, корреляционный анализ, прикладная программа MSExcel.
Грамотное владение математическим языком существенно расширяет профессиональные и коммуникативные возможности современного образованного человека. Уровень профессиональной подготовки будущих бакалавров физической культуры должен соответствовать тем высоким требованиям, которые предъявляет им современное общество. Качество образования зависит от многих составляющих, в том числе и от образовательных моделей, используемых в процессе профессиональной подготовки. Согласно проведенным исследованиям, каждый студент избирателен в способах получения и переработки информации, что обеспечивается ведущей репрезентативной сенсорной системой, своевременное выявление и учет которой повысит эффективность вербальной и невербальной коммуникации. Ведущей сенсорной системой у студентов вузов физической культуры в большей мере является кинестетическая, что обусловливает использование на занятиях современных информационных технологий.
В связи с этим в современном тренировочном процессе применяются новые современные, автоматизированные средства и методы исследования, а, следовательно, возникла необходимость в использовании современных информационных технологий и математических знаний при решении научно-исследовательских в области физической культуры и спорта. Математические методы с использованием информационных технологий дают будущим специалистам — практикам мощный, хорошо разработанный аппарат для объективного анализа результатов измерений и выработки практических рекомендаций по совершенствованию спортивной подготовки.
В связи с этим, в учебный план магистратуры по направлению 49.04.01 «Физическая культура» в вариативную часть блока 1 (дисциплины по выбору) вошла такая дисциплина как «Компьютерные технологии обработки и анализа результатов измерений в области физической культуры и спорта», изучаемая в третьем семестре 2 курса обучения.
Основной целью изучения дисциплины «Компьютерные технологии обработки и анализа результатов измерений в области физической культуры и спорта» является формирование профессиональных компетенций, применяемых для объективного анализа спортивных результатов, а также результатов педагогического, медицинского, психологического обследований и выработке практических рекомендаций по совершенствованию спортивной подготовки. Данный курс дисциплины предусматривает проведение лекционных, практических занятий и особое внимание уделяется самостоятельной работе студентов. Решение учебных задач предусматривает не только применение математических методов, но и использование табличного редактора MS Excel.
Так, при изучении темы: «Статистическое исследование зависимостей. Корреляционный и регрессионный анализ» решаются задачи требующие объемных и рутинных математических расчетов, которые занимают большой объем учебного времени, которого не хватает на акцентуацию сути решаемой проблемы. В связи с этим использование табличного редактора MS Excel при решении практических задач позволяет сократить время технических расчетов и тем самым дает возможность более детально интерпретировать результаты исследований.
Рассмотрим применение табличного редактора MS Excel на примере определения направления, формы и тесноты взаимосвязи с помощью построения графика корреляционного поля и расчета нормированного коэффициента корреляции Пирсона между результатами в беге на 30 и 100 м у 20 исследуемых.
Пример.
В результате проведенного тестирования в беге на 30 и 100 м у исследуемых получены следующие результаты (таблица № 1)
Таблица 1
Результаты тестирования в беге на 30 и 100 м у исследуемых
|
4,6 |
4,8 |
4,9 |
4,7 |
4,6 |
4,8 |
4,7 |
4,9 |
5,0 |
4,7 |
4,9 |
4,8 |
4,9 |
4,7 |
4,8 |
5,0 |
4,7 |
4,6 |
4,9 |
4,7 |
|
|
Yi, с |
12,4 |
13,1 |
13,5 |
13,1 |
12,5 |
13,3 |
13,2 |
13,7 |
13,7 |
13,0 |
13,6 |
13,2 |
13,5 |
13,2 |
13,3 |
13,7 |
13,1 |
12,4 |
13,5 |
13,0 |
Необходимо построить график корреляционного поля, отложив по оси Х, в порядке возрастания результаты в беге на 30 метров, а по оси У — результаты в беге на 100 метров.
Решение.
- Занесем полученные результаты в таблицу.
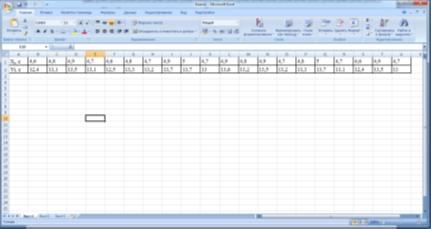
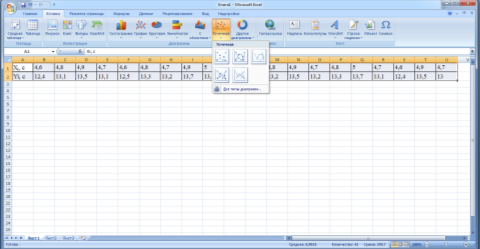
- Строим корреляционное поле. Для этого выделяем данные в таблице и на главной ленте выбираем вкладку ВСТАВКА (ТОЧЕЧНАЯ С МАРКЕРАМИ), щелкнем на выбранный график.
- Получаем график.
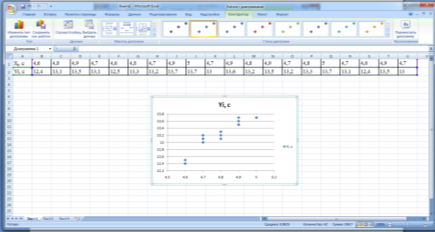
- Делаем вывод о форме и направлении взаимосвязи между исследуемыми показателями: график данного корреляционного поля позволяет предположить, что возможно, между результатами в беге на 30 и 100 метров у исследуемой группы наблюдается прямая и положительная взаимосвязь, т. е. со снижением показателя времени в беге на 30 метров будет происходить повышение результатов в беге на 100 метров.
Приступаем к решению второй части задачи — расчету нормированного коэффициента Пирсона по формулe:
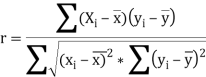
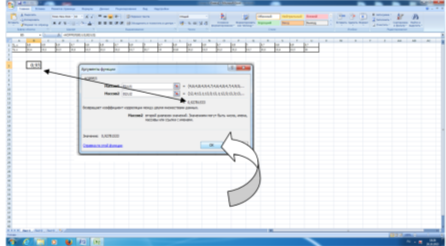
- Используя данные исходной таблицы, выделяем свободную ячейку и с помощью команды МАСТЕР ФУНКЦИЙ выбираем функцию КОРРЕЛ в разделе СТАТИСТИЧЕСКИЕ.
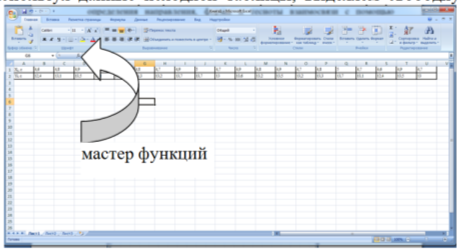
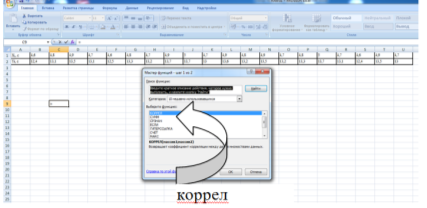
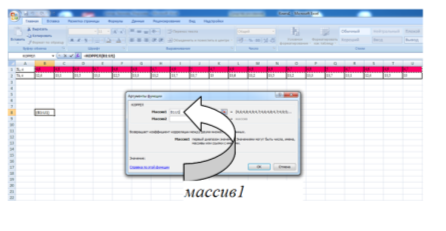
В появившемся диалоговом окне, в строке массив1, выделяем строку, соответствующую значениям Хi.
Затем щелкаем в строке массив2 и выделяем строку, соответствующую значениям Yi.
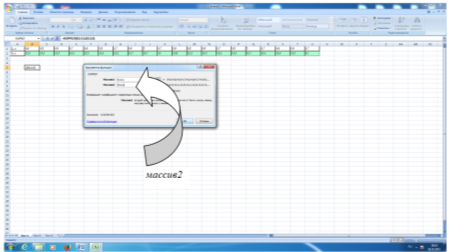
После проведенных действий кликаем на кнопку ОК и в выделенной ячейке появляется значение искомого коэффициента корреляции. В нашем случае оно равно 0,93.
Затем необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для числа степеней свободы k = n — 2 и уровня значимости α = 1 %. Если rрасч.≥rтабл., то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если rрасч.˂ rтабл., то между признаками наблюдается недостоверная корреляционная связь.
Делаем вывод:
- Так как rрасч.= 0,93˃0, то между данными выборок наблюдается прямая положительная взаимосвязь, то есть со снижением показателя времени в беге на 30 метров будет происходить повышение результатов в беге на 100 метров.
- Так как rрасч.=0,93˃rтабл. = 0,56 для k = 18 при α = 1 %, то с уверенностью β = 99 % можно говорить о том, что выявленная зависимость достоверна.
Таким образом использование современных информационных технологий в преподавании дисциплины «Компьютерные технологии обработки и анализа результатов измерений в физической культуре и спорте» позволяет сократить время, затраченное на технические математические расчеты и тем самым увеличить число практических задач, решаемых на одном аудиторном занятии. Это позволяет выработать устойчивые умения и навыки при решении задач данного типа.
Литература:
- Леонова Ирина Васильевна. Оптимизация процесса естественнонаучной подготовки специалистов по физической культуре и спорту: 13.00.08 Леонова, Ирина Васильевна Оптимизация процесса естественнонаучной подготовки специалистов по физической культуре и спорту (На примере физики): Дис.... канд. пед. наук: 13.00.08 Майкоп, 2006 187 с.
- Леонова И. В. Оптимизация процесса естественнонаучной подготовки специалистов по физической культуре и спорту (На примере физики): автореферат дис.... кандидата педагогических. наук: 13.00.08 / Адыгейский государственный университет — Майкоп, 2006, 25 с.
-
Мирзоева В. В. и др. Математические методы и модели в экономике: Учебник / С. Н. Грицюк, В. В. Лысенко — Ростов н/Д: Феникс, 2007. — 348 с.
- Мирзоева Е. В. Профилизация процесса естественно-научной подготовки студентов вузов физической культуры: На примере математики: автореферат дис.... кандидата педагогических наук: 13.00.04 / Кубан. гос. ун-т физ. культуры, спорта и туризма — Краснодар, 2006 — Количество страниц: 25 с.
- Мирзоева Елена Владимировна. Профилизация процесса естественно-научной подготовки студентов вузов физической культуры: 13.00.04 Мирзоева, Елена Владимировна Профилизация процесса естественно-научной подготовки студентов вузов физической культуры (На примере математики): Дис.... канд. пед. наук: 13.00.04 Краснодар, 2006 175 с.
