Известно, что в плазме вакуумного дугового разряда микрокапли подвергаются воздействию плазменных компонент, в результате чего может происходить как нагрев капли, так и её охлаждение. В настоящей работе проведено исследование возможности испарения капельной фазы с размером частицы диаметром 0,4 мкм и ниже при сообщении дополнительной энергии плазме. При расчёте теплового состояния частицы в плазме применялись модели пылевой плазмы, а также данные об излучательной способности субмикронных тел.
Ключевые слова: вакуумная дуга, дуговой испаритель, микрокапли, капля, капельная фаза, испарение, плазма
В последнее время всё более актуальным становиться вопрос применения износостойких, упрочняющих, коррозионно-устойчивых покрытий. Одним из наиболее востребованных и распространённых способов осаждения таких покрытий является вакуумно-дуговой способ [1]. Данный метод дает значительный выигрыш в скорости роста осаждаемого покрытия по сравнению с другими способами плазменного осаждения покрытий, обладает высокой энергоэффективностью и позволяет управлять свойствами покрытий. Недостатком технологии является наличие микрокапельной фазы в потоке плазмы разряда — микрочастиц катода, оседающих на поверхности детали. Присутствие этих частиц в покрытии могут значительно снизить качественные показатели покрытия.
Данные микрочастицы на подложке имеют диаметр от 30 нм до 10 мкм [2, 5,7,8]. Средняя скорость движения капель от 20 до 200м/c в пролётной области, её значение может варьироваться, главным образом, в зависимости от материала катода и плотности плазмы. [10, 11]
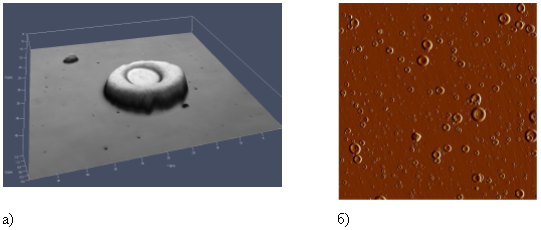
Рис.1 Трехмерный (а) и двухмерный (б) снимок поверхности образца с медным покрытием, нанесённым вакуумно-дуговым методом
Для снижения доли микрокапельной фазы в плазме вакуумно-дугового разряда используют электростатические или магнитные сепараторы плазмы [12, 13]. Однако такой подход более чем в 10 раз снижает эффективность метода, а так же усложняет и удорожает вакуумно-дуговые установки. Другим, менее эффективным способом снижения массы капельной фазы, является увеличение скорости движения катодных пятен с помощью арочного магнитного поля [3, 12, 4, 5]. При движении в арочном магнитном поле наблюдается существенная неравномерность выработки катода, что требует организации управления катодных пятен [3, 4, 5]
В работе [14] рассматривается принципиальная возможность уменьшения доли микрокапель в плазменном потоке вакуумной дуги за счёт их нагрева и испарения под действием потоков заряженных частиц на пути от катода до подложки. Для расчета теплового баланса капли учитывались мощности передаваемые капле электронной и ионной компонентами плазмы, а также взаимодействие капли с нейтральными компонентами плазмы. Было показано, что существует возможность нагрева и испарения капель размером до 10 мкм. В работе [15] приведён расчёт теплового баланса капли только с учётом взаимодействия микрочастицы с электронной и ионной компонентами плазмы. Тепловое излучение капли не учитывалось, но были учтены процессы испарения атомов с поверхности капли в процессе её движения до подложки.
Целью данной работы является оценка возможности уменьшения доли микрокапельной фазы посредством сообщения микрокаплям в объеме плазмы дополнительной мощности для их испарения. Расчёт теплового баланса микрокапли проводился с учётом наработок в области модели пылевой плазмы, а также с учётом данных по излучению микро и нанообъектов.
Физическая модель
Микрокапли двигаются от поверхности катода по направлению к подложке сквозь плазму вакуумной дуги и подвергаются воздействию электронов и ионов плазмы. Это обуславливает заряд частиц до амбиполярного потенциала, определяемого параметрами плазмы. Приходящие потоки мощности, передаваемые микрокапле электронной и ионной компонентами плазмы, приводят к её нагреву, но в то же время тепловое излучение с поверхности микрочастицы и испарение атомов приводит к её остыванию. Доля энергии, отводимой от капли излучением, может быть значительна ввиду возможных высоких температур капли — вплоть до нескольких тысяч градусов. Общая схема тепловых потоков на поверхности частицы представлена на рисунке 2.
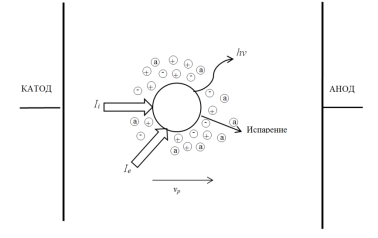
Рис. 2 Общая схема тепловых потоков на поверхности микрочастицы
Микрокапли, находящиеся в межэлектродном зазоре в плазме дугового разряда, электрически изолированы друг от друга и приобретают определённый плавающий потенциал под действием электронного и ионного токов. Таким образом, условия существования микрокапель и микрочастицы в пылевой плазме схожи, и, следовательно, для оценки состояния микрокапли (заряд, токи заряженных частиц) могут быть применены модели, разработаные для расчёта пылевой плазмы. [16, 17, 18].
Для теплового расчёта сначала необходимо задать начальную температуру капли, скорость её движения, размер и параметры плазмы, в которой капля движется. Начальная температура капли неизвестна, и её определение является достаточно трудной задачей. При оценке начальной температуры капли следует учитывать, что катод является интегрально холодным, с оплавленной поверхностью, а капли приходят на подложку в жидком состоянии. То есть температура капли больше температуры плавления, но, скорее всего, значительно ниже температуры кипения. В процессе движения капли от катода к подложке капля может, как нагреваться, так и остывать. Для определённости примем, что температура капли имеет температуру плавления материала. В качестве материала капли примем алюминий. Температура плавления алюминия составляет 933 К, температура кипения — 2792 К. Скорость электронов в плазме принималась равной ve= 1×106 (соответствует температуре 6 эВ), скорость движения ионов vi= 1,25×104 м/с [15, 18]. Для определённости в дальнейшем расчёте примем, что скорость движения капель составляет 100 м/с. Наибольшую массовую долю в потоке плазмы имеют капли с диаметром 1 мкм [23]. При осаждении их на подложку в форме диска высота капли составляет 30 нм. Таким образом, примем радиус капли a = 0,175 мкм.
Модель взаимодействия частиц с заряженными частицами в пылевой пылевой плазмы справедлива при допущении, что диаметр частицы гораздо больше радиуса экранирования Дебая и гораздо меньше, чем длина свободного пробега электронов или ионов:
![]() (1)
(1)
Примем, что параметры плазмы вокруг капли не изменяются во время её движения. В таком случае радиус экранирования
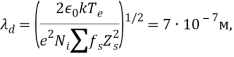 (2)
(2)
где ![]() - диэлектрическая проницаемость среды в вакууме,
- диэлектрическая проницаемость среды в вакууме, ![]() — доля частиц с зарядом типа s, имеющих ионизированность
— доля частиц с зарядом типа s, имеющих ионизированность ![]() ,
, ![]() — концентрация ионов в плазме разряда,
— концентрация ионов в плазме разряда, ![]() - температура электронов в плазме,
- температура электронов в плазме, ![]() - постоянная Больцмана,
- постоянная Больцмана, ![]() — заряд электрона.
— заряд электрона.
Длины свободного пробега заряженных частиц ![]() составили для электронов и ионов соответственно:
составили для электронов и ионов соответственно:
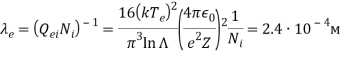 (3)
(3)
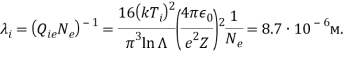
Плотность тока J должна вычисляться из условия стационарного горения дугового разряда, так как мы рассматриваем состояние капли в объёме плазмы. В таком случае необходимо брать общую рабочую площадь катода на которой существует разряд. Таким образом, плотность тока J составляет
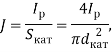 (4)
(4)
где ![]() — ток разряда, dкат — диаметр катода.
— ток разряда, dкат — диаметр катода.
Для катодного пятна дуги общий ионный ток представляет собой постоянную часть f от общего тока дуги [19]. Тогда концентрация ионов и электронов в плазме описываемого разряда будет составлять:
![]()
где e- заряд электронов, Z=2 — средний заряд иона [20], vi — скорость ионов, ![]() - плотность ионного тока дуги, J — плотность тока дуги.
- плотность ионного тока дуги, J — плотность тока дуги.
Таким образом, условие (3) выполняется. Значит, вклад электронного и ионного токов в изменение внутренней энергии капли будет составлять
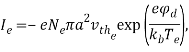 (6)
(6)
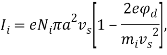 (7)
(7)
где ![]() — плавающий потенциал микрокапли; mi — масса иона; kb — постоянная Больцмана; Те и
— плавающий потенциал микрокапли; mi — масса иона; kb — постоянная Больцмана; Те и ![]() – температура электронов и ионов соответственно,
– температура электронов и ионов соответственно, ![]() и
и ![]() — концентрация ионов и электронов в плазме, vs — дрейфовая скорость ионов,
— концентрация ионов и электронов в плазме, vs — дрейфовая скорость ионов, ![]() — средняя тепловая скорость электронов.
— средняя тепловая скорость электронов.
Плавающий потенциал микрокапли вычисляется с помощью выражения [14]:
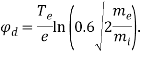 (8)
(8)
В (6) и (7) было принято, что распределение частиц по энергиям теплового движения является максвелловских, и скорость направленного движения ионов больше скорости теплового движения [16].
Охлаждение микрокапли за счет излучения описывается законом Стефана-Больцмана, следовательно, ![]() можно выразить следующим образом:
можно выразить следующим образом:
![]() (9)
(9)
где a — радиус микрокапли,
Микрокапли имеют значительную температуру, но размеры большей части микрокапель менее 1 мкм. По данным [21, 22], при субмикронных размерах объекта излучательная способность тела значительно уменьшается. Таким образом, вклад излучения в тепловой баланс будет значительно меньше, чем в случае, если не вводить поправку на излучательную способность субмикронных тел. Согласно данным [22] примем, что излучательная способность поверхности капли составляет 0.05.
Проводя аналогию между взаимодействием микрочастицы пылевой плазмы и микрокапли с плазмой разряда, мощности, передаваемые микрокапле электронной и ионной компонентами плазмы можно описать так [20]:
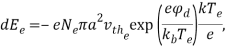
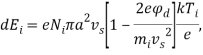 (10)
(10)
где ![]() — плавающий потенциал микрокапли; mi — масса иона; kb — постоянная Больцмана; Те и
— плавающий потенциал микрокапли; mi — масса иона; kb — постоянная Больцмана; Те и ![]() – температура электронов и ионов соответственно,
– температура электронов и ионов соответственно, ![]() и
и ![]() — концентрация ионов и электронов в плазме, vs — дрейфовая скорость ионов,
— концентрация ионов и электронов в плазме, vs — дрейфовая скорость ионов, ![]() — средняя тепловая скорость электронов.
— средняя тепловая скорость электронов.
Дрейфовая скорость ионов определяется как [21]:
![]()
![]()
![]() ,
,
где vd — скорость капли, ![]() — степень неидеальности ионной компоненты плазмы, Z — зарядовое число материала капли, Тi — температура ионов в энергетических единицах.
— степень неидеальности ионной компоненты плазмы, Z — зарядовое число материала капли, Тi — температура ионов в энергетических единицах.
Средние тепловые скорости ионов и электронов вычисляются как:
![]()
![]() (11)
(11)
Параметр неидеальности Г является одной из основных характеристик системы многих взаимодействующих частиц, которую необходимо учитывать. Г, определяется как отношение потенциальной энергии взаимодействия между соседними частицами к их средней кинетической энергии [20, 21]. Для заряженных частиц
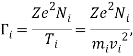 (12)
(12)
Изменение внутренней энергии ![]() , капли можно описать так:
, капли можно описать так:
![]() =
=![]() , (13)
, (13)
где с=903 ![]() — удельная теплоемкость материала капли (алюминий),
— удельная теплоемкость материала капли (алюминий), ![]() = 1.4∙10–15 кг — масса капли рассматриваемого диапазона.
= 1.4∙10–15 кг — масса капли рассматриваемого диапазона.
Расчёт
В расчёте будем считать, что подводимая извне энергия идёт на изменение внутренней энергии капли ![]() , которая ведёт к её нагреву, либо остыванию. Общий вид уравнения теплового баланса капли можно записать так:
, которая ведёт к её нагреву, либо остыванию. Общий вид уравнения теплового баланса капли можно записать так:
![]() (14)
(14)
где
Таким образом, общее дифференциальное выражение для теплового баланса микрокапли будет иметь вид:
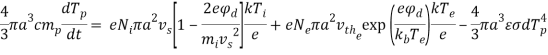 (15)
(15)
Правая часть уравнения (15) будет описывать поток энергии на поверхность капли:
![]() (16)
(16)
Для заданных начальных условий при постоянной температуре поток тепла на каплю со стороны плазмы P0=3.54∙10–7 Вт. Зная поток энергии на частицу, можно определить, какой удельный поток массы испаряется с неё при нагреве [15,6]:
![]() , (17)
, (17)
где М –молярная масса вещества в а. е.м., mp — масса протона, P0- подводимая к частице мощность, ![]() — энергия испарения, приходящейся на один атом микрокапли. Для заданных начальных и граничных условий
— энергия испарения, приходящейся на один атом микрокапли. Для заданных начальных и граничных условий
В тоже время, для испарения всей капли, за время её полета от катода к подложкее при расстоянии между ними, скажем,L=1м за время ![]() с необходимо, чтобы поток массы с капли составлял 0.044
с необходимо, чтобы поток массы с капли составлял 0.044 ![]() :
:
![]() (18)
(18)
где ![]() — площадь капли,
— площадь капли, ![]() — масса капли.
— масса капли.
Зная необходимый поток массы с капли, можно рассчитать мощность, которую нужно вложить в неё для обеспечения такого потока. Из (17) имеем:
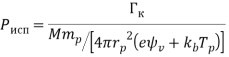 (19)
(19)
Для заданных условий мощность ![]() , необходимая для испарения капли размером 0,36 мкм составляет P0=0.145Вт, что значительно больше, чем мощность, подводимая к капле со стороны плазмы. При этом мощности, поступающей на каплю со стороны плазмы, достаточно лишь для испарения капель размером не более 40 нм.
, необходимая для испарения капли размером 0,36 мкм составляет P0=0.145Вт, что значительно больше, чем мощность, подводимая к капле со стороны плазмы. При этом мощности, поступающей на каплю со стороны плазмы, достаточно лишь для испарения капель размером не более 40 нм.
Таким образом, было показано, что мощности, подводимой к капле со стороны плазмы достаточно для испарения капель только размером несколько десятков нанометров. Для испарения капель большего размера в плазму необходимо вводить дополнительную мощность.
Выводы
В работе был проведён расчёт теплового состояния микрокапли в плазме вакуумного дугового разряда, оценён вклад электронной и ионной компоненты в тепловой баланс капли, а также проведена оценка дополнительной мощности, необходимой для испарения осадившейся на подложке капли размером 1 мкм. При расчёте применялась модель состояния частицы в пылевой плазме и модель излучения субмикронных тел. Было показано, что мощности, подводимой к капле со стороны плазмы, недостаточно, чтобы испарить или хотя бы заметно снизить размеры капли.
Литература:
- Духопельников Д. В., Жуков А. В., Кириллов Д. В., Марахтанов М. К. Структура и особенности движения катодного пятна вакуумной дуги на протяженном титановом катоде//Измерительная техника. 2005. № 10. С. 42–44.
- Духопельников Д. В., Кириллов Д. В., Булычёв В. С. Характеристики кремниевых микрокапель в покрытиях, осаждённых методом вакуумного дугового испарения // Все материалы. Энциклопедическийсправочник. 2015. № 12, с. 18–24.
- Swift P. D., McKenzie D. R., Falconer I. S. Cathode spot phenomena in titanium vacuum arcs // J. Appl. Phys., 66 (2), 1989, p. 505–512.
- Духопельников Д. В., Жуков А. В., Кириллов Д. В., Марахтанов М. К. Структура и особенности движения катодного пятна вакуумной дуги на протяжённом титановом катоде // Измерительная техника. 2003. № 10. С. 42–44.
- Духопельников Д. В., Кириллов Д. В., Щуренкова С. А. Динамика движения катодных пятен по поверхности катода в поперечном магнитном поле//Наука и образование. МГТУ им. Н. Э. Баумана. Электрон. журн. 2012. № 1. Режим доступа: http://technomag.edu.ru/doc/256359.html (дата обращения 10.11.2015).
- Духопельников Д. В., Кириллов Д. В., Рязанов В. А., Чжо Вин Наинг. Оптимизация траектории движения катодного пятна для повышения равномерности выработки катода вакуумного дугового испарителя//Инженерный журнал: наука и инновации. 2013. № 10 (22). С. 42. Режим доступа: http://engjournal.ru/catalog/machin/plasma/1042.html (дата обращения 10.12.2015).
- Духопельников Д. В., Кириллов Д. В., Марахтанов М. К., Воробьев Е. В., Булычёв В. С. Вакуумная дуга на поликристаллическом кремниевом катоде. // Наука и образование: научное издание МГТУ им. Н. Э. Баумана. 2014. № 11. С. 188–197. Режим доступа: http://technomag.bmstu.ru/doc/748209.html (дата обращения 05.06.2015).
- Кириллов Д. В., Рязанов В. А. Исследование профиля выработки катода дугового испарителя при различных токах разряда и индукции магнитного поля // Молодежный научно-технический вестник. 2013. № 5. С. 18.
- Дэшман С. Научные основы вакуумной техники. М.: Изд-во «Мир», 1964. 716 с.
- McClure G. W. Plasma expansion as a cause of metal displacement in vacuum arc spots // J. Appl. Phys. -1974. -Vol.45. -№ 5.-P. 2078–2084
- Utsumi T and English J H 1975 Study of electrode products emittedby vacuum arcs in form of molten metal particles J. Appl. Phys. 46 126–3
- Takikawa, H.; Tanoue, H. Review of Cathodic Arc Deposition for Preparing Droplet-Free Thin Films. IEEE Trans. Plasma Sci. 2007, 35 (4), 992–999
- І. І. Аксьонов, В. А. Білоус Вакуумно-дугове обладнання для йонно-плазмового осадження покриттів (огляд) (укр.) // «Вопросы Атомной Науки и Техники» (ВАНТ): Журнал. — Харьков: Национальный научныйцентр «Харьковский физико-технический институт», 2000. — № 4. — С. 153–157. — ISBN нет, УДК546.25.-162. — ISSN 1562–6016.
- Бизюков А. А., Ромащенко Е. В., Середа К. Н., Чибисов А. Д., Кашаба А. Е. Динамика капельной фазы в плазме дугового разряда низкого давления// «Вестник Харьковского университета», № 642, 2004. Режим доступа: http://www-nuclear.univer.kharkov.ua/lib/642_3(25)_04_p4246.pdf (дата обращения 15. 12.2015).
- R. L. Boxman and S. Goldsmith, J. Appl. Phys. 51, 3644 (1980).
- В. Е. Фортов, А. Г. Храпак, С. А. Храпак, В. И. Молотков, О. Ф. Петров, “Пылевая плазма”, УФН, 174:5 (2004), 495–544
- Morfill G. E., Thomas H., J. Vac. Sci. Technol. A, 14 (1996), 490
- W. D. Davis and H. C. Miller, J. Appl. Phys. 40, 2212 (1969).
- C. W. Kimblin, J. Appl. Phys. 44, 3974 (1973).
- А. С. Дикалюк, С. Т. Суржиков. Учет процесса зарядки твердых частиц при моделировании эволюции пылевой компоненты плазмы в нормальном тлеющем разряде // Физико-химическая кинетика в газовой динамике, 2, 2011, с.1–9.
- Yat-Yin Au, Helgi Skuli Skulason, Snorri Ingvarsson, Levente J. Klein, and Hendrik F. Hamann Thermal radiation spectra of individual subwavelength microheaters // PHYSICAL REVIEW B 78, 085402 2008. DOI: http://journals.aps.org/prb/abstract/10.1103/PhysRevB.78.085402 (дата обращения: 15.12.2015)
- Мартыненко Ю. В., Огнев Л. И. Тепловое излучение наночастиц. — ЖТФ, 2005, т. 75, вып. 11, с. 130–132.
- Гранкина О. О., Гранкина Т. О. Исследование поверхностной плотности микрокапель в титановых покрытиях, полученных в вакуумно-дуговом испарителе с арочным магнитным полем // Молодёжный научно-технический вестник, электронный журнал, 2015. — № 2, http://sntbul.bmstu.ru/doc/760856.html, дата обращения: 29.10.2015.







