Введение дополнительных избыточных степеней подвижности — один из эффективных путей оптимизации движений манипулятора. В работе рассматривается совершенствование стратегии управления малыми движениями конечной точки манипулятора в терминах минимизации, мощности и максимизации ускорения двухзвенного плоского механизма. Анализ показал, что при введенных ограничениях ни одна конструкция механизма не обеспечивает одновременно максимизации ускорения и минимизации потребной мощности.
Ключевые слова: манипулятор, управление, кинематическая избыточность
Представлена стратегия максимального расширения полосы пропускания двухзвенного механизма малых движений в одном направлении.
Для этого случая избыточность понимается в том смысле, что малые движения в направлении 
, как показано на рис.1, могут достигаться путем изменения по определенному закону углов 
за счет введения соответствующих управляющих воздействий. Разрабатываемая стратегия включает в себя распределение движения между 
и 
, а также оптимальный выбор длин звеньев 
и 
Система рассматривается как линейная, поскольку не учитываются кориолисовы силы и центробежные ускорения. Это предположение допустимо в окрестности номинальной конфигурации 
. Линейный под ход позволяет также использовать постоянные преобразования между параметрами движения сочленений и движением выходного звена, а так же между параметрами движения сочленений и действующими в них крутящими моментами.
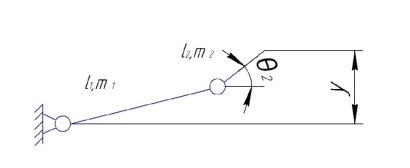
Рис. 1. Кинематическая схема
Качество системы будет измеряться шириной поносы возможных синусоидальных колебаний конечной точки механизма. В общем случае это компромисс между точностью абсолютного положения манипулятора и абсолютной величиной усилия, которое зависит от импеданса манипулятора и окружающей его среды. Увеличение полосы пропускания должно повысить эффективность управления, как по усилию, так и по положению. Это особенно важно для быстрой коррекции ошибок в этих контурах управления.
Исследуется поведение механизма в окрестностях номинальной конфигурации , которая является центром рабочей области для движения с избыточностью. Величина рабочей зоны выбирается с цепью ограничения углового перемещения звена 2 относительно звена 1 так, что
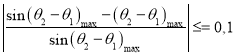(1)
Ограничение 
позволяет использовать линейные методы анализа, а также ограничивает величину отклонений от номинальной конфигурации, вызванных влиянием возмущений» Введенное определение малых движений ограничивает величину перемещений по оси у величиной + 5 % общей длины механизма. Рассматриваются два подхода к улучшению динамических характеристик. Первый включает поиск условий минимальных затрат мощности на синусоидальное движение концевой точки механизма. Мгновенное значение потребной мощности для синусоидального движения постоянной амплитуды и частоты со определяется из выражения
(2)
- симметрическая матрица моментов инерции звеньев относительно центров шарниров
Альтернативный подход к улучшению рабочих характеристик механизма связан с поиском возможного максимума ускорения в направлении .
Для механизма, показанного на рис. 1, ускорение концевой точки находится из уравнения
(3)
Конструирование механизма начинается с выбора относительного движения двухзвенного механизма. Простейший, метод состоит в определении постоянной, связывающей движения в двух шарнирах. Для максимизации характеристик, описанных уравнениями (2) и (3), предлагается использовать коэффициенты оптимальной угловой скорости в шарнирах, исходя из параметров механизма. Процедура точного определения длин звеньев механической системы с избыточностью строится на совместном использовании оптимальных угловых коэффициентов и рассмотренных выше ограничений. Вводится обозначение углового коэффициента 
. Это обозначение остается справедливым и для производных от 
и 
. Для фиксированного значения амплитуды концевой точки 
(4)
Ограничив в уравнении (2) переменные
и полученные из уравнения (4), и продифференцировав его по 
, можно определить угловой коэффициент 
, минимизирующий величину потребной мощности при движении концевой точки механизма по синусоидальному закону с постоянной амплитудой
(5)
Определим 
как коэффициент углового ускорения, полученный для фиксированных значений передаточных отношений 
и 
крутящих моментов на валах двигателей 
и 
(6)
Выбор постоянных угловых коэффициентов позволяет использовать линейные методы анализа.
Объединив уравнения (4), (2) и (3) и продифференцировав по 
можно показать, что минимум энергетических затрат и максимум ускорения достигаются в пределе, когда стремится к нулю. Следовательно, выбор будет зависеть от следующих ограничений, накладываемых на систему: угловой коэффициент 
; фиксированная длина механизма 
; малое перемещение; максимальное угловое перемещение. Нижняя допустимая граница находится, из выражения
(7)
Таким образом, оптимальная длина звеньев — это наименьшая длина, удовлетворяющая данным критериям ускорения или мощности с учетом ограничений, выраженных уравнением (7).
Выбор параметров системы должен производиться на основе критериев, минимизирующих потребную мощность и максимизирующих ускорение, Предполагается, что масса тонких цилиндрических звеньев двухзвенного плоского механизма пропорциональна их длине. Введение матрицы П позволяет учесть влияние приведенного момента инерции двигателя, Кроме критериев рабочих характеристик, выраженных уравнениями (2) и (3), для определения полного набора конструктивных параметров учитываются ограничения по уравнению (7), Эти уравнения решаются для трех различных случаев.
- Однозвенная система, которая представляется как базис для сравнения характеристик различных конструкций двухзвенных механизмов
-
Выбор конструктивных параметров механизма на основе минимизации потребляемой мощности. Для этого используется уравнение (2). На первом этапе учитывается только инерционность звена. Уравнение (2) может быть нормализовано (L=1) и выражено в терминах
.
-
Выбор параметров механизма путем определения максимума ускорения концевой точки в направлении
- Выбор параметров механизма на основе комбинированного критерия.
В случаях 2 и 3 ускорение концевой точки определялось главным образом угловым ускорением второго звена. В предположении постоянства коэффициента углового ускорения 
крутящий момент в шарнире 2 можно выразить
(8)
где
эффективный момент инерции двигателя второго звена.
Трактуя звено 2 как скалярную систему, можно подобрать 
. Можно выбрать приведенные крутящие моменты двигателей так, чтобы для данной статической нагрузки требовались равные крутящие моменты двигателей т. е.
(9)
Выбор приведенных моментов инерции 
по уравнению (9) обеспечивает равное возбуждение двигателей каждого звена. При этом оба двигателя одновременно достигают предела насыщения крутящего момента. В этом случае достигается равенство 
. Таким образом, наиболее эффективное движение механизма имеет место при равном возбуждении обоих двигателей. Представленные в работе расчетные параметры конструкции двухзвенного механизма выше, чем параметры однозвенного механизма для режиме малых перемещений. Отмечается наличие альтернативных вариантов в выборе методов оптимизации. Стандартный подход к конструированию механизма — поиск максимума ускорения. При этом приведенный момент инерции двигателя каждого звена согласуется с моментом инерции звеньев, и к каждому звену подводится равное количество энергии. Результирующее движение требует больших перемещений сочленения 1.
Минимизация потребной мощности рациональна при выборе 
и 
. При этом резко уменьшается частота включения двигателя звена 1. Таким образом, случай 4 сочетает в себе достоинства обоих методов. Максимизация углового ускорения движения в сочленении 2 обеспечивает высокое ускорение, а выбор низкого значения приведенного крутящего момента двигателя звена 1 уменьшает общую потребную мощность для данного движения. Правильный выбор приведенного момента инерции (уравнение (9)) приводит к такой конструкции, в которой управляемый крутящий момент обеспечивает одновременно максимум ускорения и движение с наивысшим к. п.д.
Для реализации преимуществ избыточности, обеспечивающих высокую частоту отработки управляющих сигналов при движении по оси , предлагается метод, использующий оптимальный угловой коэффициент 
. Для этого первоначально определяется тип матрицы Якоби, на основе которой проводятся достоверные измерения и управление внешними и внутренними движениями механизма. Вблизи
отклонение в направлении представляется в виде:
. Поскольку движение в направлении х невозможно, якобиан представляется вырожденной матрицей. Выражение для нулевого или внутреннего движения имеет вид: 
. Движение в пространстве сочленений ортогонально к отклонению . Это позволяет движение в пространстве сочленений 
преобразовать во внешнее движение
, с помощью невырожденной матрицы Якоби
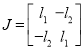(10)
Это преобразование имеет вид: 
Вводится дополнительное 
- пространство. Движение в направлении оси 
системы координат этого пространства требует, чтобы движение системы характеризовалось 
. В этом случае движение в направлении будет эффективным, а движение вдоль оси 
неэффективным. Определив 
и
(12)
можно определить преобразование пространства в пространство сочленения как
(13)
На рис.2 показаны базовые векторы двух пространств. Пространство сочленений 
используется как исходная система координат. Эффективное выполнение движений в направлении требует управления отклонением в направлении . Причем движение по требует больших отклонений в направлении 
. Для разрешения этого противоречия рассматривается эллипс 
на рис.2. Каждая точка эллипса представляет множество скоростей сочленения, удовлетворяющих уравнению
(14)
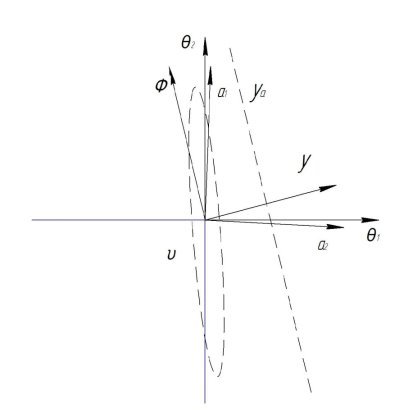
Рис. 2.
где Е — постоянный уровень энергии. Точки на эллипсе представляют скорости в пространстве сочленения, достижимые при фиксированном количестве энергии. Для данного количества энергии большие скорости могут достигаться вдоль главной оси этого эллипса, а не по направлению. Однако это направление обеспечивает малые отклонения по . Таким образом, направление, полученное на основании уравнения (5), обеспечивает наилучшее соотношение скоростей, при котором достигается отклонение концевой точки механизма в направлении с наименьшей потребной мощностью.
Линия 
на рис.2 представляет собой геометрическое место точек необходимых перемещений шарнира для достижения перемещения на которые накладываются различные по величине нулевые отклонения. Для достижения этих отклонений следует двигаться в направлении до момента достижения . Далее система управления компенсирует нулевую составляющую и возвращает механизм к положению, при котором 
. [1–3]
Анализ показал, что при введенных ограничениях ни одна конструкция механизма не обеспечивает одновременно максимизации ускорения и минимизации потребной мощности. В некоторой степени это требование может удовлетворяться введением, дополнительных сочленений.
Литература:
- Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч./ Е. В. Поезжаева. — Пермь Изд-во Пермь.гос, тех. ун-та, 2006.- Ч.1.-64 с.
- Зенкевич С. Л., Ющенко А:.С. Управление роботами.- М.:Изд-во МГОУ им. Н. Э. Баумана, 2006.
- Корендясев А. И. Теоретические основы робототехники: в 2 кн./ А. И. Корендясев, Б. Л. Саламандра, Л. И. Тывес; отв. Ред. С. М. Каплунов.– М.:Наука,2006.
