In today's world, an important issue in favor the safety and security of people. The most important is to protect the population from attacks. These crimes are not acceptable, therefore, created a robot designed to detect and destroy explosive devices.
Keywords: robot, the mobility, the linearized model, the dynamic parameters.
Задачи по созданию мобильных роботов, способных выявлять и уничтожать взрывчатые устройства имеет успех за рубежом. В Европейских странах имеется большой опыт ведения антитеррористической борьбы. В России подобный опыт не так велик. Но в последнее время в нашей стране высокий риск терактов, поэтому мы создали робота который справится с обнаружением и ликвидацией взрывчатых устройств.
Основным назначением мобильного робота является визуальная, а также акустическая разведка местности, зданий, машин, труднодоступных мест, выявление и ликвидация взрывчатого устройства. Малогабаритный робот оснащается быстросъемным рабочим оборудованием.

Рис.1. Малогабаритный робот с многофункциональным назначением
В робота включены сенсоры, манипулятор, пульт управления, колесная платформа, разрушитель взрывчатых устройств. Робот оснащается трехосной полноприводной платформой. Машина может передвигаться по слабопересеченной местности, преодолевать водные преграды и препятствия. Манипулятор обладает несколькими степенями свободы и включает в себя механизмы гидродинамического разрушителя взрывчатого устройства и наведения видеокамеры. Обследователь труднодоступные места, находить и уничтожать объекты позволяет выдвижная телескопическая штанга.
Уничтожение взрывчатого устройства производится с помощью гидродинамического выстрела, который превышает скорость детонирования, что позволяет избежать взрыва. Также робот имеет специальный контейнер, в который можно сбросить взрывчатое устройство, отвезти на безопасное расстояние и произвести подрыв.
Робот может зарекомендовать себя в реальных условиях эксплуатации, решает задачи, связанные с обнаружением и ликвидацией взрывчатых устройств. Отличительной особенностью предлагаемой конструкции, для которой разрабатывалась динамика является маневренность при его эксплуатации.
Вывод уравнений динамики робота со многими степенями подвижности представляет собой сложную трудоемкую задачу. В связи с этим, а также с целью исключения ошибок вычисления разработаны программные системы, осуществляющие построение динамической модели робота в символьном виде. Рассматривается процедура автоматизированного вывода линеаризованных уравнений динамики робота в форме уравнений Лагранжа и одновременно исследуется чувствительность движения манипулятора к изменению его параметров.
Динамическими параметрами манипулятора являются матрицы псевдоинерции звена, вектор центра масс звена и масса звена. Вектор сил тяжести в координатной системе основания робота означается g= [gxgygz0]T
Рассмотрим разложение первого порядка уравнений динамики относительно номинальной траектории (q0, q̇0, q̈0). Линеаризованная динамическая модель робота имеет вид
D0δq̈ + 2Sv0δq̇+{S0D+Sc0+SG0}δq=δF(t) (1)
Поскольку силы инерции связаны с ускорением в степенях подвижности линейной зависимостью, свойства матрицы чувствительности D0 совпадают со свойствами матрицы инерционных коэффициентов D(q). Матрица D0 является положительно определенной и неособенной.
По произведенным оценкам формирование полной линеаризованной динамической модели наиболее распространенных типов манипулятора требует в несколько раз больше затрат машинного времени по сравнению с выводом динамической модели робота в символьном виде.
Рассматриваем свойства и функциональные зависимости матриц чувствительности. Все элементы матрицы чувствительности являются функциями номинальных значений всех обобщенных координат и не зависят от номинальных скоростей и ускорений.
Линеаризованная модель (1) может быть представлена в виде системы 2N уравнений в пространстве состояний
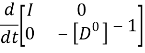
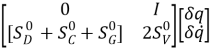
+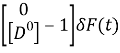 (2)
(2)
илиδẋ=A(t)δx(t)+B(t)δu(t) (3)
Здесь 2N переменных состояния δx линеаризованной модели включают δx линеаризованной модели включают N отклонений δq и N скоростей δq̇. Матрицы А и В изменяются во времени, поскольку матрицы чувствительности определяются на изменяющейся во времени номинальной траектории.
Функции чувствительности характеризуют отклонение относительно номинальной траектории обобщенных координат и их скоростей при вариациях существенных параметров манипулятора.
Входные сигналы определяются выражением
![]() (4)
(4)
где σ= [σj]- вектор чувствительности обобщенных координат; σ̇= [σ̇j]-вектор чувствительности скорости; u(t)-вектор входного сигнала.
Подавая сигнал на вход системы с нулевыми начальными условиями, можно получить изменение функции чувствительности на номинальной траектории.
Полученные результаты могут быть использованы для оценки влияния вариации массы объекта манипулирования на движение манипулятора. Пусть JNPи JNE- соответственно матрицы псевдоинерции нагрузки и рабочего органа. Тогда матрица псевдоинерции N-го звена равна
JN=JNP+JNE(5)
Элементы матрицы JNPмогут изменяться при работе с разными объектами либо при вариациях захвата однотипных объектов.
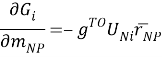 (6)
(6)
Данное уравнение представляет собой входной сигнал ui(t) для модели чувствительности. Подавая этот сигнал на вход линеаризованной динамической модели можно найти чувствительность траектории к изменению массы объекта манипулирования.
Описанные выше процедуры включены в состав программной системы Arm, позволяющей формировать в символьном виде описание динамики манипуляционных роботов и проводить исследования в машинных экспериментах.
Литература:
- Поезжаева Е. В. Промышленные роботы: учебное пособие в 3 ч. — М.; УМО АМ МВТУ им. Баумана; изд-во ПГТУ, 2009.
- http://bibliofond.ru/view.aspx?id=655956







