Блочно-операторная матрица — это матрица, элементы которой являются линейными операторами в банаховом или гильбертовом пространствах [1]. Одним из специальных классов блочно-операторных матриц являются Гамильтонианы системы с несохраняющимся числом квантовых частиц на целочисленной решетке. Их количество может быть неограниченным, как в случае моделей спин-бозонов [2,3] или ограниченным, как в случае урезанных моделей спин-бозонов [4,5]. Отметим, что такие системы обычно возникают в задачах физики твердого тела [6], квантовой теории поля [7], статистической физики [8], магнитогидродинамики [9] и квантовой механики [10].
В настоящей работе рассматривается блочно-операторная матрица ![]() (обобщенная модель Фридрихса), ассоциированная с системой не более, чем двух, квантовых частиц на
(обобщенная модель Фридрихса), ассоциированная с системой не более, чем двух, квантовых частиц на ![]() –мерной решетке. Описывается его существенный и дискретный спектры. Найдены условия существования собственных значений.
–мерной решетке. Описывается его существенный и дискретный спектры. Найдены условия существования собственных значений.
Пусть ![]() –
– ![]() –мерный тор, т. е. куб
–мерный тор, т. е. куб ![]() — с соответствующим отождествлением противоположных граней. Всюду в работе
— с соответствующим отождествлением противоположных граней. Всюду в работе ![]() рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в ![]() по модулю
по модулю ![]() , где
, где ![]() и
и ![]() - множество вещественных и целых чисел, соответственно. Например, если
- множество вещественных и целых чисел, соответственно. Например, если ![]() и
и
![]() ,
,
то
![]() .
.
Пусть ![]() — одномерное комплексное пространство и
— одномерное комплексное пространство и ![]() — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на ![]() . Символом
. Символом ![]() обозначается прямая сумма пространств
обозначается прямая сумма пространств ![]() и
и ![]() , т. е.
, т. е. ![]() . Пространства
. Пространства ![]() и
и ![]() называются нольчастичным и одночастичным подпространствами фоковского пространства, соответственно.
называются нольчастичным и одночастичным подпространствами фоковского пространства, соответственно.
Хорошо известно, что любой линейный ограниченный оператор ![]() , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве ![]() , всегда представляется как блочно-операторная матрица
, всегда представляется как блочно-операторная матрица ![]()
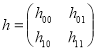 ,(1)
,(1)
где матричные элементы
![]() .
.
В настоящей работе рассмотрим случай, когда операторы ![]() в формуле (1), определяются равенствами:
в формуле (1), определяются равенствами:
![]() ,
,
![]() .
.
При этом ![]() — фиксированное вещественное число,
— фиксированное вещественное число, ![]() и
и ![]() вещественнозначные непрерывные функции на
вещественнозначные непрерывные функции на ![]() , а
, а ![]() сопряженное оператор к
сопряженное оператор к ![]() и
и
![]() .
.
Полученный оператор обычно называется обобщенная модель Фридрихса и является ограниченным и самосопряженным.
Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
В математической физике оператор ![]() называется оператором уничтожения, а оператор
называется оператором уничтожения, а оператор ![]() называется оператором рождения.
называется оператором рождения.
Обозначим через ![]() ,
, ![]() и
и ![]() , соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
, соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Пусть оператор
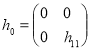 .
.
Оператор возмущения ![]() оператора
оператора ![]() является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора
является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора ![]()
![]() совпадает с существенным спектром оператора
совпадает с существенным спектром оператора ![]() . Известно, что
. Известно, что
![]() ,
,
где числа ![]() и
и ![]() определяются следующим образом:
определяются следующим образом:
![]() .
.
Из последних фактов следует, что ![]() .
.
Определим регулярную в ![]() функцию (детерминант Фредгольма, ассоциированный с оператором
функцию (детерминант Фредгольма, ассоциированный с оператором ![]() )
)
![]() .
.
Следующая лемма установит связь между собственными значениями оператора ![]() и нулями функции
и нулями функции ![]() .
.
Лемма 1. Число ![]() является собственным значением оператора
является собственным значением оператора ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Доказательство. Пусть число
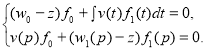 (2)
(2)
Так как ![]() , из второго уравнения системы (1) для
, из второго уравнения системы (1) для ![]() имеем
имеем
![]() . (3)
. (3)
Подставляя выражение (3) для ![]() в первое уравнение системы (2) заключаем, что система уравнений (2) имеет ненулевое решение тогда и только тогда, когда
в первое уравнение системы (2) заключаем, что система уравнений (2) имеет ненулевое решение тогда и только тогда, когда ![]() . Лемма 1 доказана.
. Лемма 1 доказана.
Из леммы 1 вытекает, что
![]() .
.
Таким образом
![]() .
.
Так как функция ![]() является строго убывающей на полуосях
является строго убывающей на полуосях ![]() и
и ![]() , то отсюда и из теоремы о предельном переходе под знаком интеграла Лебега следует, что существуют пределы (конечное или бесконечное)
, то отсюда и из теоремы о предельном переходе под знаком интеграла Лебега следует, что существуют пределы (конечное или бесконечное)
![]() ;
;
По определению ![]() и
и ![]() .
.
Лемма 2.Оператор ![]() имеет единственное собственное значение, лежащее на
имеет единственное собственное значение, лежащее на ![]() ,
, ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Доказательство. Пусть ![]() ,
, ![]() –собственное значение оператора
–собственное значение оператора ![]() . В силу леммы 1 это означает, что
. В силу леммы 1 это означает, что ![]() . Так как для любого
. Так как для любого ![]() имеет место соотношение
имеет место соотношение
![]() ,
,
функция ![]() монотонно убывает на полуосях
монотонно убывает на полуосях ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() .
.
Обратно. Пусть для некоторого ![]() выполняется неравенство
выполняется неравенство ![]() . Так как
. Так как ![]() и функция
и функция ![]() монотонна и непрерывна в полуоси
монотонна и непрерывна в полуоси ![]() , то существует единственное число
, то существует единственное число ![]() такое, что
такое, что ![]() . По лемме 1 число
. По лемме 1 число ![]() – является собственным значением оператора
– является собственным значением оператора ![]() . Лемма 2 доказана.
. Лемма 2 доказана.
Следующая лемма доказывается аналогично.
Лемма 3.Оператор ![]() имеет единственное собственное значение, лежащее на
имеет единственное собственное значение, лежащее на ![]() ,
, ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Таким образом имеет место следующая теорема.
Теорема 1.
а) Если
б) Если ![]() , то оператор
, то оператор ![]() имеет единственное собственное значение на
имеет единственное собственное значение на ![]() ;
;
в) Если ![]() , то оператор
, то оператор ![]() не имеет собственных значений на
не имеет собственных значений на ![]() ;
;
г) Если ![]() , то оператор
, то оператор ![]() имеет единственное собственное значение на
имеет единственное собственное значение на ![]() .
.
Доказательства теоремы 1 вытекает из леммы 2 и 3.
Следствие. Если ![]() и
и ![]() , то оператор
, то оператор ![]() имеет два собственных значений
имеет два собственных значений ![]() , причем
, причем ![]() и
и ![]() .
.
Литература:
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. Imperial College Press, 2008.
- H. Spohn. Ground states of the spin-boson Hamiltonian. Comm. Math. Phys., 123 (1989), 277–304.
- M. Huebner, H. Spohn. Spectral properties of the spin-boson Hamiltonian. Ann. Inst. Henri Poincare, 62:3 (1995), 289–323.
- Ю. В. Жуков, Р. А. Минлос. Спектр и рассеяние в модели «спин-бозон» с не более чем тремя фотонами. Теор. и матем. физика, 103:1 (1995), 63–81.
- R. A. Minlos, H. Spohn. The three-body problem in radioactive decay: the case of one atom and at most two photons. Topics in Statistical and Theoretical Physics, American Mathematical Society Translations–Series 2, 177 (1996), 159–193.
- A. I. Mogilner. Hamiltonians in solid state physics as multiparticle discrete Schroedinger operators: problems and results. AdvancesinSov. Math. 5 (1991), 139–194.
- К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.
- V. A. Malishev, R. A. Minlos. Linear infinite-particle operators. Translations of Mathematical Monographs. 143, AMS, Providence, RI, 1995.
- A. E. Lifschitz. Magnetohydrodynamic and spectral theory. Vol. 4 of Developments in Electromagnetic Theory and Applications. Kluwer Academic Publishers Group, Dordrecht, 1989.
- B. Thaller. The Dirac equation. Texts and Monographs in Physics. Springer, Berlin, 1992.







