К теории устойчивости вращающейся плазмы с постоянным градиентом температуры

 

В статье исследуется устойчивость конвективного течения в неоднородно вращающейся цилиндрической плазме в аксиальном однородном магнитном поле. В приближении геометрической оптики получено дисперсионное уравнение для малых осесимметричных возмущений с учетом эффектов вязкости, омической и теплопроводной диссипации. Найдены критерии устойчивости течений плазмы, при нарушении которых, возникает новый тип конвективной магнитовращательной неустойчивости.

Ключевые слова: магнитовращательная неустойчивость; дисперсионное уравнение; алгоритм Раусса — Гурвица; конвективные течения; критические числа Рэлея.

 

1. Введение

Исследование эффектов вращения в электропроводящих средах играет важную роль для технических применений, например в термоядерных установках [1], в устройствах по накоплению энергии, в плазменных центрифугах [2].

Теоретическим исследованиям устойчивости вращающихся электропроводящих сред (плазме и т. п.) в слабых магнитных полях посвящено огромное число работ (например, обзоры [3–7]). Здесь следует отметить и об астрофизических приложениях данной проблемы. В частности, переоткрытая в работах [8, 9] магнитовращательная неустойчивость (МВН) применялась для объяснения происхождения турбулентности плазмы в аккреционных дисках. За долго до работ [8, 9], в работе [10], была описана неустойчивость неоднородно вращающейся в осевом магнитном поле абсолютно электропроводящей жидкости. В дальнейшем исследование устойчивости вращающейся плазмы проводилось с учетом влияния различных факторов. Так, в работах [11, 12] подробно исследовалось влияние эффектов вязкости и магнитной диффузии на устойчивость неоднородно вращающейся плазмы. Кроме того, в работах [12, 13] учитывалась радиальная стратификация плазмы, нетривиальная топология внешнего магнитного поля, т. е. ненулевая спиральность этого поля: . В последних работах [14, 15] были получены критерии развития МВН для разряженной плазмы при учете эффектов Холла и диссипации.

Хорошо известно, что свободная конвекция несжимаемой жидкости при вертикальном подогреве является абсолютно неустойчивой [3]. В связи с этим, возникает вопрос об устойчивости неоднородно вращающейся плазмы в однородном магнитном поле и при вертикальном подогреве в постоянном гравитационном поле. Именно данной проблеме посвящена настоящая работа. Результаты, полученные в настоящей работе, могут иметь практическое значение как для ряда астрофизических задач, так и для лабораторных исследований.

2. Основные уравнения и постановка задачи

Рассмотрим вращающуся проводящую среду (плазму) в постоянном гравитационном и магнитном полях при постоянном градиенте температуры. Конвективные явления, вызванные градиентом температуры, описываются уравнениями движения вязкой несжимаемой электропроводящей жидкости в приближении Буссинеска [16]:

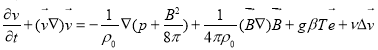(1)

(2)

где - кинематическая вязкость, - единичный вектор, направленный вертикально вверх по оси , - коэффициент теплового расширения, , - постоянный градиент температуры (его знак меняется от условий подогрева), - плотность среды, - коэффициент теплопроводности среды. Уравнения (1), (2) дополним уравнениями индукции магнитного поля и условиями соленоидальности полей и :

(3)

, (4)

Основной нашей задачей является вопрос об устойчивости малых возмущений физических величин, эволюция которых описывается системой уравнений (1)-(4). Для решения этой проблемы будем использовать цилиндрическую систему координат , выбор которой обусловлен возможностью практического применения развиваемой здесь теории. Пусть плазма находится в однородном магнитном поле , направленным вдоль оси вращения , и вращается в азимутальном направлении со скоростью , где - угловая скорость вращения, являющаяся произвольной функцией радиуса. Система уравнений (1)-(4) имеет стационарные решения вида:

, , , ,

,, (5)

Для такого течения в радиальном направлении устанавливается центробежное равновесие:

,

а в вертикальном — гидростатическое:

В линейном приближении, возмущенные решения представим в виде:

, , ,

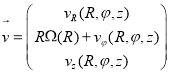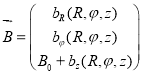(6)

После подстановки (6) в систему уравнений (1)-(4), и последующей линеаризации, получим основные уравнения для исследования устойчивости малых возмущений.

Рассмотрим предел слабой стратификации среды, когда характерный масштаб неоднородности (стратификации) 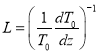намного превышает характерный масштаб возмущений : . В этом случае выполняется приближение геометрической оптики [17] и поэтому возмущенные величины можно представить в виде плоских волн с пространственно-временной зависимостью вида:, где и -радиальная и аксиальная проекции волнового вектора , - инкремент возмущений. Здесь мы также рассматриваем осесимметричные возмущения, для которых . Тогда линеаризованная система дифференциальных уравнений (1)-(4) сводится к алгебраической из которой мы получим дисперсионное уравнение следующего вида:

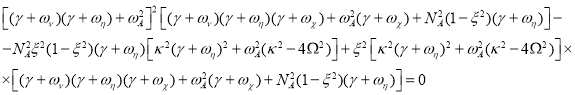(7)

В уравнении (7) введены обозначения для вязкостной , омической и теплопроводной частоты, , - альфвеновская частота, , - частота Вяйселя-Брента на градиенте температуры, , .

Дисперсионное уравнение (7) после несложных алгебраических преобразований расщепляется на два дисперсионных уравнения следующего вида:

(8)

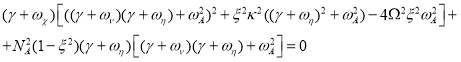(9)

Дисперсионное уравнение (8) описывает затухание альфвеновских волн в плазме с вязкой и омической диссипацией. В этом уравнении отсутствует влияние вращения и температурной стратификации на инкремент возмущений, поэтому представляет интерес анализ дисперсионного уравнения (9), в котором это влияние содержится.

Нетрудно заметить, что уравнение (9) содержит в себе результаты, ставшие уже классическими. Например, при отсутствии вращения и магнитного поля в случае непроводящей среды получаем дисперсионное уравнение, описывающее свободную конвекцию Рэлея [16]:

(10)

Переходя к безразмерным переменным , и учитывая (- целое число, характеризующее масштаб по вертикали), решение уравнения (10) имеет вид [16]:

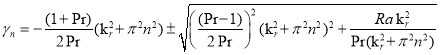(11)

Величина инкремента неустойчивости зависит от безразмерных чисел Рэлея , Прандтля и волнового числа. Условием устойчивости малых возмущений является положительность подкоренного выражения, что соответствует числам Рэлея .

Если среда однородная по температуре (), бездиссипативная и вращается с угловой скоростью (течение Куэтта) при отсутствии магнитного поля, то из уравнения (9) мы получим известный критерий неустойчивости Рэлея (см. например обзор [4]):

(12)

Для идеально проводящих сред, Велиховым [10] было показано, что магнитное поле дестабилизирует течение Куэтта. Критерий неустойчивости для этого случая обобщает результат (31):

(13)

Учет только вращения и магнитного поля в однородной диссипативной среде преобразует уравнение (9) к дисперсионному уравнению следующего вида:

(14)

Уравнение (14) подробно исследовалось в работе [11], а его обобщение с учетом радиальной тепловой стратификации среды в работах [12, 13]. В отличие от работ [12, 13], в полученном нами дисперсионном уравнении (9) учтена тепловая диссипация (члены с ) и вертикальная стратификация (члены с ) по температуре в поле тяжести. Фактически это означает, что мы рассматриваем свободные конвективные движения неоднородно вращающейся плазмы в постоянном магнитном поле.

3. Анализ устойчивости вращающейся плазмы с постоянным градиентом температуры

Раскрывая скобки в уравнении (9), получим окончательный вид дисперсионного уравнения в виде полинома пятой степени относительно инкремента :

, (15)

где коэффициенты имеют соответствующий вид:

, ,

,

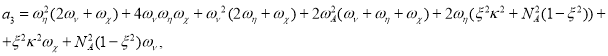
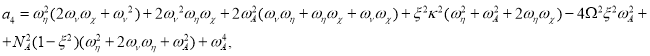
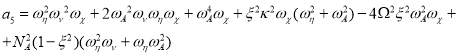(16)

Критерии асимптотической устойчивости возмущений, описываемых алгебраическим уравнением (15), можно получить, применяя алгоритм Рауса-Гурвица или Льенара-Шипара. Суть алгоритма состоит в следующем [18]: для того чтобы многочлен имел все корни с отрицательными вещественными частями, необходимо и достаточно, чтобы

а) все коэффициенты многочлена были положительны: , ;

б) имели место неравенства для определителей Гурвица: , …, где - обозначает определитель Гурвица - порядка:

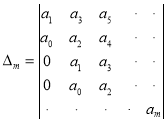
Используя алгоритм Рауса-Гурвица получим необходимые и достаточные условия устойчивости неоднородно вращающейся плазмы с постоянным градиентом температуры:

, , , . (17)

Здесь определители и соответственно равны:

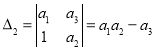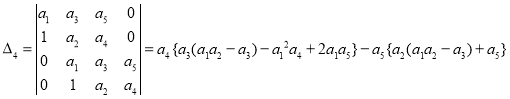, (18)

Подставляя значения коэффициентов , определяемые соотношениями (16), в условия (17) находим следующие неравенства:

1)        () - это неравенство выполняется автоматически;

2)        () — отсюда видно, что вязкая, омическая и теплопроводностная диссипация естественно приводят к стабилизации устойчивости течений плазмы. Кроме того, стабилизирующими факторами выступают однородное магнитное поле (альфвеновский эффект), неоднородное вращение, если профиль угловой скорости вращения близок к (), а также градиент температуры при (подогрев снизу). В пределе бездиссипативной и однородной электропроводящей жидкости в однородном магнитном поле это неравенство переходит в известный критерий устойчивости Велихова [1];

3)        неравенство не содержит новых условий стабилизации возмущений;

4)        (), где введены обозначения для диссипативных членов: , , , . В бездиссипативном случае и однородной плазмы () условие устойчивости 4) принимает упрощенный вид [13]:

При наличии диссипации в условии 4) видно появление дестабилизирующего члена, который играет существенную роль для малых значений магнитного поля , и является причиной возникновения МВН.

5)        .

Переходя к безразмерным переменным в неравенстве 5) условие устойчивости конвективных течений плазмы принимает простой вид: , где - критическое число Рэлея, соответствующее точке () на нейтральной кривой, разделяющей области устойчивости и неустойчивости возмущений. Значение критического числа Рэлея равно:

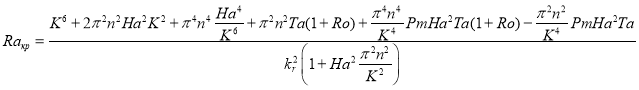(19)

Отсюда видно, что критические числа Рэлея зависят не только от волновых чисел , но и от безразмерных параметров среды: магнитного числа Прандтля , числа Гартмана , числа Тейлора , числа Россби . Для твердотельного вращения параметр Россби равен нулю , в случае кеплеровского вращения , для профиля угловой скорости соответственно .

Выражение (19) содержит уже известные результаты из монографии [3] в различных предельных случаях. Так, для не вращающейся и не электропроводной жидкости (, ) критические числа Рэлея, как известно, равны [3, с. 37] , а минимальное его значение при равно . В случае твердотельного вращения (, ) непроводящей жидкости (,) [3, с. 210]: , не вращающейся () проводящей жидкости [3, с. 194]: .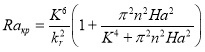

Перейдем теперь к условиям устойчивости б), состоящим из неравенств с определителями Гурвица (18). Для определителя получаем:

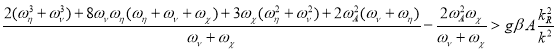(20)

В этом неравенстве появился новый дестабилизирующий член (вторая дробь), оказывающий существенное влияние при условии малости чисел Прандтля . При условии и происходит стабилизация возмущений магнитным полем в диссипативной среде. После подстановки значений коэффициентов в выражение для определителя Гурвица мы получим последнее из условий устойчивости: . Явный вид неравенства мы не приводим из-за громоздкого вида входящих в него выражений. Однако заметим, что критерий устойчивости содержит в себе предыдущий критерий устойчивости (20).

Заключение

В настоящей работе с помощью алгоритма Раусса-Гурвица исследовались критерии устойчивости неоднородно вращающейся плазмы в аксиальном однородном магнитном поле при вертикальном подогреве в поле силы тяжести. При нарушении этих критериев устойчивости, в плазме возможно появление нового типа конвективной магнитовращательной неустойчивости (КМВН). В результате развития КМВН происходит рост амплитуд возмущений, образуются когерентные структуры (типа конвективных ячеек), совершающие хаотические движения, переходящие в турбулентность. Естественно, в этом случае начинают важную роль играть нелинейные эффекты. Однако, уже в рамках линейной теории мы видим при каких физических условиях развивается неустойчивость. Дальнейший анализ КМВН следует проводить в рамках нелинейной теории, но это не входило в круг задач, рассматриваемых в настоящей работе, и поэтому будет рассматриваться в следующих работах.

 

Литература:

 

1.      Федотовский В. С., Логинов Н. И., Михеев А. С., Верещагина Т. И., Тереник Л. В., Прохоров Ю. П. Экспериментальная установка для исследования магнитовращательной неустойчивости // Пути ученого. Е. П. Велихов. Под общ. ред. ак. В. П. Смирнова. М.: РНЦ «Курчатовский институт», Москва, 2007. С. 167–175.
2.      Карчевский А. И., Потанин Е. П. Плазменные центрифуги. Изотопы. Свойства, получение, применение. М.: ФИЗМАТЛИТ, 2005.
3.      Shakura N., Postnov K. On properties of Velikhov-Chandrasekhar MRI in ideal and non-ideal plasma. ArXiv: 1412.1223v1 [astro-ph. HE] 3 Dec. 2014.
4.      Шалыбков Д. А. Гидродинамическая и гидромагнитная устойчивость течения Куэтта // УФН. 2009. Т. 179. № 9. С. 971–993.
5.      Михайловский А. Б., Ломинадзе Дж. Г., Чуриков А. П., Пустовитов В. Д. Прогресс в теории неустойчивостей вращающейся плазмы // Физика плазмы. 2009. Т. 35. С. 307–350.
6.      Rudiger G., Kitchatinov L., Hollerbach R. Magnetic Processes in Astrophysics. Theory, Simulation, Experiments. Wiley-VCH Verlag GmbH & Co. KGaA. 2013. P. 346.
7.      Kirillov O., Stefani F. Standard and helical magnetorotational instabilty. ArXiv: 1109.1940v1 [astro-ph.SR] 9 Sep. 2011.
8.      Balbus S. and Hawley J. A powerful local shear instability in weakly magnetized disk. I. Linear analysis // Astrophys. J. 1991.V. 376.P. 214–222.
9.      Papaloizou J. and Szuszkiewich E. The stability of a differentially rotating disk with a poloidal magnetic field // Geophys. Astrophys. Fluid. Dyn. 1992. V. 66. P. 223–242.
10. Велихов Е. П. Устойчивость течения идеально проводящей жидкости между вращающимися цилиндрами в магнитном поле // ЖЭТФ. 1959. Т. 36. С. 1398–1404.
11. Goodman J. and Ji H. Magnetorotational instability of dissipative Couette flow// J. Fluid. Mech. 2002. V.462. P. 365–382.
12. Лахин В. П., Ильгисонис В. И. О влиянии диссипативных эффектов на неустойчивости дифференциально-вращающейся плазмы // ЖЭТФ. 2010. Т. 137. Вып. 4. С. 783–788.
13. Лахин В. П. Неустойчивости и волны во вращающейся плазме и турбулентная генерация регулярных структур // Дисс. на соиск. уч. степ. доктора физ.-мат. наук. Москва: НИЦ «Курчатовский институт» 2013. 257 с.
14. Горшунов Н. М., Потанин Е. П. Влияние холловских эффектов на устойчивость вращающейся плазмы // Успехи прикладной физики. 2013. Т. 1. № 2. С. 178–182.
15. Горшунов Н. М., Потанин Е. П. Границы устойчивости вращающейся вязкой плазмы в магнитном поле // Успехи прикладной физики. 2014. Т. 2. № 1. С. 18–23.
16. Гершуни Г. З., Жуховицкий Е. М. Конвективная устойчивость несжимаемой жидкости. М.: Наука. 1972. 392 с.
17. Михайловский А. Б. Теория плазменных неустойчивостей. Т. 2. Неустойчивости неоднородной плазмы. М.: Атомиздат. 1971. 312 с.
18. Гантмахер Ф. Р. Лекции по аналитической механике. М.: ФИЗМАТЛИТ. 2005. 264 с.