Definition:If 
at stubborning 
equality done this stubborning be named to involution.
This 
as functions organize involution.
Look at following equation
(1)
Here 
involution that is 
free term.
On the bottom (1) well, we will show made unraweling (1) inequality
involution been 
make a change:
(2)
For extense 
get. This is not delivery hurt for totall. We, in the bottom (2) from equality
will found together 
. That, made up this equality.
(3)
This equal
then, we will increasing.
In that
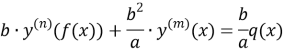(4)
be crop this equality.
Third and fourth equality spearated. In result:
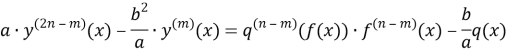(5)
be crop this equality. Well, (5) equality (1) this shown. That equality to be help, then simple differencial made up equation.
Examples:
-
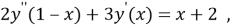
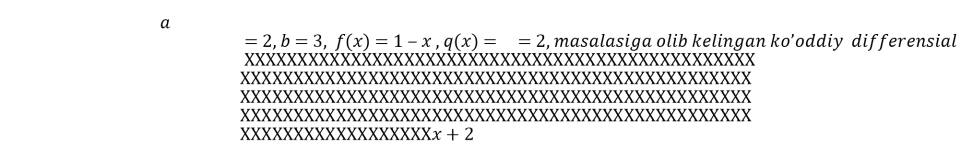been. n=2, m=1 we use this values then made up equation.
(n-m)=1, (2n –m)=3.Well, there are to (5).The result:
(6)
be crop this equalition.
this equality total value its one of own value and its one gender part composed of total together.
We will find one fender part’s total unravelling:
,made up carasteristic equality
from than 
Well, the total unravelling’s one gender of part composed of this:
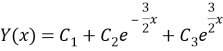
b) (6) we will take off one own unraveling this equality:
searching. In shown it is to (6) take put in
from
, d- voluntary number.
Well (6) unraveling private equality.
Well, (6) in equality total unraveling.
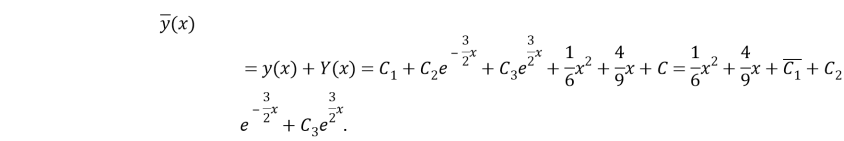(7)
(7) untying (6) the total unravelling.
2.
. We (n-m)=2,
(2n-m)=5,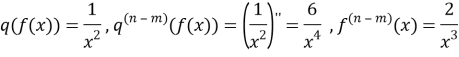 
There are to (5) put on. Result:
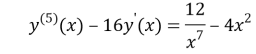(8)
be crop this equality.
(8) this equality unraveling same before the xample. We could set free this equality from involution.
Conclusion: With us, well in (1) equality 
stage of numbers to tied funcsions should,came too.
But, unraveling this kind of examples came to difficult direction.
But, this kind of equality:
(9)
we could unraveling. Well, been position 
. In this 
, 
are to dendent on funcsions.(9) equality (1) we should look at this unraveling as equality’s state.
References:
- Винер И. Я. Дифференциальные уравнения с инволюциями. // Дифференциальные уравнения. Том 5, 1969.
- Хромов А. П. Смешанная задача для дифференциального уравнения с инволюцией и потенциалом специального вида. // Известия Саратовского университета, Нов.сер. Математика, Механика, Информатика. 2010,,т.10. вып № 4,с.17–22.
