Атомные электростанции — это наше будущее. Вопросы безопасности — одна из ключевых задач строителей и инженеров-проектировщиков. Должны быть применены инновационные конструкции и современные технологии, которые позволят избежать каких-либо неприятностей. При строительстве и реконструкции объектов АЭС возникает необходимость в экономически эффективных оболочках различного назначения: трубопроводы, охладители, мини-емкости.
Инновационная тонкостенная полая оболочка создается из двухслойной заготовки, образованной из двух полос скрепленных шовной сваркой или клеящим составом [1] с последующим ее деформированием избыточным давлением. Анализ проведенных экспериментов [1, 2] показал, что две полосы под воздействием внутреннего давления, приобретают вид цилиндрической оболочки полого поперечного сечения, образование которого сопровождается большими пластическими деформациями. После снятия давления проектная форма цилиндрической оболочки сохраняется (рис.1) и имеет высокую несущую способность.
Теоретическое обоснование упруго-пластического деформирования полос сопряжено с большими трудностями, поэтому введем следующие допущения: свойства материала описываются диаграммой ![]() ; сжимаемостью материала пренебрегается; рассматривается стадия активного нагружения; деформации считаются умеренно большими; перемещения срединной поверхности формируемой оболочки большие. Решение задачи формообразования оболочки сводится к решению задачи цилиндрического изгиба стальной полосы при больших перемещениях. Физические уравнениясвязи напряжений и деформаций в плоском напряженном состоянии [3] запишем в виде:
; сжимаемостью материала пренебрегается; рассматривается стадия активного нагружения; деформации считаются умеренно большими; перемещения срединной поверхности формируемой оболочки большие. Решение задачи формообразования оболочки сводится к решению задачи цилиндрического изгиба стальной полосы при больших перемещениях. Физические уравнениясвязи напряжений и деформаций в плоском напряженном состоянии [3] запишем в виде:
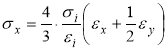 ;
; ![]() ,
,
где ![]() - интенсивность деформации и напряжений;
- интенсивность деформации и напряжений; ![]() — деформации в направлении осей х и у;
— деформации в направлении осей х и у; ![]() - напряжения в направлении осей х и у.
- напряжения в направлении осей х и у.
При цилиндрическом изгибе имеем
![]() и
и 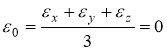 , поэтому
, поэтому ![]() ;
;
тогда имеем 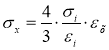 ;
; 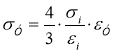 .
.
Представим уравнение диаграммы ![]() полиномом нечетной степени, ограничившись при этом двумя членами ряда,
полиномом нечетной степени, ограничившись при этом двумя членами ряда,
после преобразования напряжения определятся:
![]() , (1)
, (1)
где А и С — произвольные постоянные, определяемые экспериментально из диаграммы ![]() .
.

Рис. 1.
Задача расчета пластин с прямоугольным очертанием контура оказывается значительно более сложной, чем симметричных круглых пластин. Вызвано это, прежде всего тем, что прогибы и напряжения несимметричной пластины определяются в функции не одного, а двух независимых переменных. Для прямоугольной пластины в качестве таких переменных берутся обычно величины х и у в прямоугольной системе координат.
Вырежем из изогнутой длиной пластины (рис.2) балку-полоску единичной ширины и определим изгибающий момент, выразив его через деформации и прогибы. Здесь: а — деформированная полоса; б — элемент полосы. Линейная деформация на расстоянии z от нейтральной оси [3] равна:
 , (2)
, (2)
где ![]() – радиус кривизны нейтрального слоя; z — координата произвольного слоя.
– радиус кривизны нейтрального слоя; z — координата произвольного слоя.
Изгибающий момент, выраженный через деформации с учетом (1) и (2) будет иметь вид:
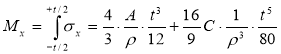 . (3)
. (3)
Радиус кривизны ![]() представим через функцию прогиба срединного слоя балки-полоски. Для больших прогибов:
представим через функцию прогиба срединного слоя балки-полоски. Для больших прогибов:
![]() . (4)
. (4)
Разложив правую часть выражения (4) в ряд Тейлора и ограничившись двумя членами ряда,
![]() .(5)
.(5)
выражение (5) преобразуем к виду:
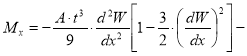
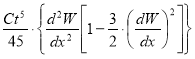 . (6)
. (6)
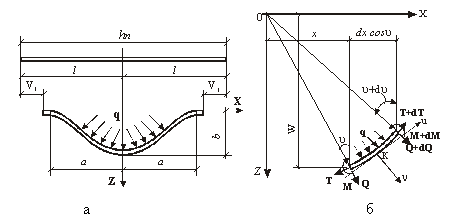
Рис. 2.
Выделив из деформированной балки-полоски (рис. 2) элемент dx и рассмотрев его равновесие с учетом пологости в пределах длины,
![]() (7)
(7)
Величину Т найдем, рассмотрев равновесие выделенного полого элемента (рис.2,б):
![]() . (8)
. (8)
Найдём связь перемещения W с углами поворота ![]() нормали. Проектируя все значения перемещений на оси Х и Z, и решая полученную систему, будем иметь:
нормали. Проектируя все значения перемещений на оси Х и Z, и решая полученную систему, будем иметь:
![]() .
. ![]() . (9)
. (9)
Представим разложение тригонометрических функций в ряды Тейлора:
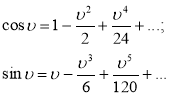
Ограничиваясь, случаем пологой кривой (рис.3), получим:
![]() ;
; ![]() . (10)
. (10)
После преобразований выражение (7) с учетом (10) принимает вид:
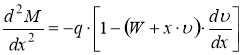 . (11)
. (11)
Решив совместно (10) и (11) с учетом (6), получим дифференциальное уравнение цилиндрического изгиба деформированной полосы:

Путем численного решения полученного уравнения методом Галеркина было найдено выражение для определения давления сжатого воздуха, необходимого формирования длинной цилиндрической оболочки полого поперечного сечения.
На основе проведенных автором экспериментальных исследований на серии моделей длинных цилиндрических оболочек из полос разных размеров и различных материалов была установлена величина избыточного давления сжатого воздуха, необходимого для формирования их полого поперечного сечения. Сравнение значений давления, полученных экспериментально и теоретически, показало достаточно хорошую сходимость — теоретическая величина избыточного давления превышает экспериментальную на 19 %...28 % [2].
Литература:
- Ращепкина С. А. Металлические емкости из легких конструкций повышенной транспортабельности / С. А. Ращепкина. — Саратов: РИЦ Сарат. гос. техн. ун-та, 2007. — 288 с.
- Ращепкина С. А. К вопросу определения параметров формообразования мини-оболочек металлических емкостей / С. А. Ращепкина // Вестник гражданских инженеров. Санкт-Петербург, 2010, № 2. С.54–60.
- Погорелов А. В. Дифференциальная геометрия. М.: изд-во «Недра». 1969. 176с.







