В работе рассмотрено моделирование распределения нагрузок по бандажной ленте турбинного колеса паровой турбины. Под влиянием различных нагрузок рабочий диск подвергается различным видам разрушений, основной из которых отрыв рабочих лопаток, бандажной ленты. Эти разрушения происходят из-за задевания о детали статора, коррозии и эрозии лопаток, трещин в лопатках, деформация и ослабление посадки на валу, ослабление крепления бандажной ленты и связующей проволоки, усталости металла, коробления, вибрации лопаток и ленточного бандажа, от степени влажности пара. При моделировании можно рассмотреть множество вариантов различных предшествующих ситуаций, но полностью избежать поломок бандажной ленты не получится. Но можно свести к минимуму внешние распределенные нагрузки на лопасть турбины.
Задачей моделирования является получение точек, имеющих максимальное напряжение разрушений бандажной ленты, для обеспечения надежной работы колеса паровой турбины.
В ходе моделирования использованы два метода: метод систем с распределенными параметрами и моделирование в программном продукте ComsolMultiphusics.
В качестве исходного уравнения при моделировании методом систем с распределенными параметрами принято уравнение колебания, отражающее свойства ленточного бандажа.
Дифференциальное уравнение имеет вид [1]:
![]()
где Q(r,t) — выходная распределенная величина, представляющая собой ортогональную деформацию кольца, Н/м2;f(r,t) — входное распределенное воздействие на бандажную ленту, Па/с2.
В нашем случае имеем граничные условия третьей краевой задачи [2]:
![]()
Так как бандажная лента крепиться на рабочие лопатки турбинного колеса с определенным интервалом между ними, то нельзя сказать, что бандажная лента жестко закреплена по внутреннему радиусу R0. Поэтому первое граничное условие приравнивается к 0.
![]()
Вторым граничным условием будет являться то, что внешний радиус R1 не имеет креплений и свободно находится в пространстве. Из этого следует, что второе граничное условие приравнивается к 0.
![]()
Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная композиция от произведения функции Грина на стандартизирующую функцию. Выходная распределенная величина рассчитывается по формуле:
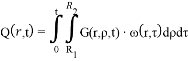
где R1 = 2.74м — максимальный радиус бандажной ленты;R0 = 2.49м — минимальный радиус бандажной ленты.
Выходная характеристика находится как сумма составляющих:
![]()
где Q1(r,t), Q2(r,t), Q3(r,t) — первая, вторая и третья составляющие выходной величины.
Подставим полученные результаты трех составляющих в общую, получим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проведем сравнение графиков напряженности, построенных в программном продукте ComsolMultiphusics методом конечных элементов и программном продукте MathCad методом систем с распределенными параметрами [3].
При моделировании напряженного состояния бандажной ленты рабочего диска паровой турбины методом конечных элементов, наиболее нагружаемыми оказались области, в которых находятся точки А и В, C и D оказались менее нагружены.
На рис.1 и рис.2 представлены графики напряженного состояния рабочего диска со значениями критических точек за время работы 24 часа.
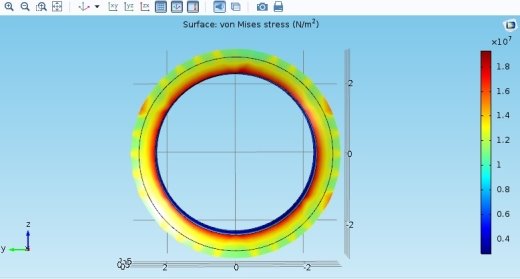
Рис. 1. Моделирование нагрузок давление пара и центробежных сил
Вид: изометрия «yz»

![]()
![]()

![]()

![]()

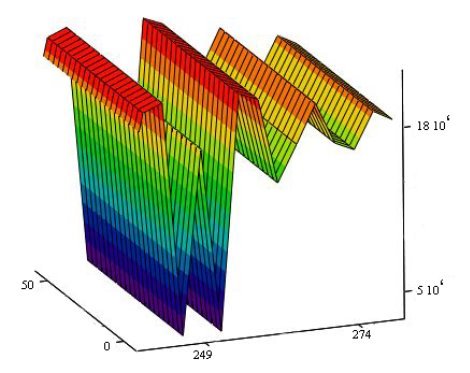
A
D
C
B
Рис. 2. График напряженности по радиусу и длине бандажной ленты
Получившиеся разными методами расчета критические точки сведем в одну таблицу для наглядного сравнения.
Таблица
Значения напряженности точек
|
Координаты точек |
Напряженность в Comsol, МПа |
Координаты точек |
Напряженность в СРП, МПа |
|
А1 (0.006; -2.086; -0.961) |
25.712 |
А2 (14; 251; 23) |
23.862 |
|
B1 (0.028; -2.110; -0.974) |
24.153 |
B2 (23; 259; 20) |
20.061 |
|
C1 (0.096;-2.188; -1.012) |
19.543 |
C2 (16; 266; 19) |
18.873 |
|
D1 (0.178;-2.303; -1.082) |
13.730 |
D2 (15; 273; 16) |
15.982 |
На основании графиков и таблицы можно сделать следующий вывод. Результаты, полученные при решении ленточного бандажа как системы с распределенными параметрами имеют некоторое отклонение от значений, полученных в программном продукте ComsolMultihpisics, выполняющий вычисления методом конечных элементов и зарекомендовавший себя как лучший программный продукт для решения нестационарных пространственных задач механики деформируемого твердого тела. Это связано с тем, что для решения системы с распределенными параметрами необходимо точно задавать граничные условия. Ленточный бандаж, как известно, имеет сложную для описания функцией форму крепления на рабочие лопатки, поэтому задание граничных условий с высокой точностью невыполнимо [4].
В качестве рекомендаций по результатам моделирования для увеличения срока работоспособности и уменьшения ремонтных работ можно предложить следующие действия: одновременное повышение качества проектирования, изготовления и эксплуатации паровых турбин. Существенным резервом повышения надежности работы лопасти и ленточного бандажа является внедрение автоматизированного нагружения, сводящего к минимуму термические напряжения, исключающие опасность задеваний в проточной части, повышающей вибрационную надежность лопаточного аппарата.
Литература:
- Бутковский А. Г. Характеристики систем с распределенными параметрами / А. Г. Бутковский. — М.: Наука, 1979. — 224 с.
- Бойко А. В. Аэродинамика проточной части паровых и газовых турбин: расчеты, исследования, оптимизация, проектирование / А. В. Бойко, А. В. Гаркуша. — Харьков, ХГПУ, 1999. -390 с.
- Норри Д. А. Введение в метод конечных элементов/ Д. А. Норли, де Фриз Ж. — М.: Мир, 1981. — 305 с.
- Скоробогатова Т. Н. Результаты моделирования распределения нагрузок по лопасти паровой турбины/ Т. Н. Скоробогатова // Информационные технологии, системы автоматизированного проектирования и автоматизации: сборник научных трудов III Всероссийской научно-технической конференции. — Саратов: СГТУ, 2011.







