В условиях рыночной экономики рациональное формирование инвестиционного портфеля позволяет инвестору получить доход и увеличить свое будущее благосостояние. Однако эффективность портфельных инвестиции напрямую зависит от способности инвесторов быстро и адекватно реагировать на изменения состояния российского финансового рынка для определения оптимальной структуры портфеля. В подобных условиях известные классические подходы [7, 9] к принятию оптимального инвестиционного решения зачастую становятся неэффективными и требуют корректировки. Применение компьютерной обработки информации для реализации моделей инвестиционного портфеля увеличивают оперативность принятия решений.
В настоящей работе рассматривается возможность модификации подхода Г. Марковица [9] с помощью фундаментальных моделей доходности [1–3, 8], оценивается эффективность данной модификации.
Основная идея портфельной теории Г. Марковица заключается в том, что координаты оптимального портфеля инвестора соответствуют точке касания его кривых безразличия эффективного множества [9]. Эффективное множество определяется Г. Марковицем как множество портфелей, которые обеспечивают минимальный риск при фиксированном уровне ожидаемой доходности, и максимальную ожидаемую доходность при определенном уровне риска [9]. Однако некоторые из предположений (например, однородность ожиданий инвесторов), на которых основывается подход Г. Марковица, не соответствуют реалиям рыночной торговли ценными бумагами, что неоднократно освещалось в ряде работ (например, в [5–6]).
В классической портфельной теории ожидаемую доходность принято определять как среднее значение фактических доходностей:
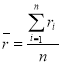, (1)
где 
— фактическая доходность актива за 
- й период времени,
— количество рассматриваемых периодов времени.
Формула (1.1) вытекает из нормального закона распределения случайных величин. Вместе с тем многочисленные исследования (например, в [4]) показывают, что доходности большинства российских финансовых активов не распределены нормально.
Методики определения ожидаемой доходности акций, известные в фундаментальном анализе основываются на изучении информации о текущем положении и перспективах развития компании, публикуемых в финансовой отчетности. Результаты данного анализа позволяют выбрать оптимальный состав портфеля ценных бумаг. В фундаментальном анализе известно несколько подходов к определению ожидаемой доходности ценных бумаг. Подробнее остановимся на наиболее известных фундаментальных моделях.
-
Определение ожидаемой доходности акций
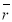через коэффициент 
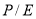[1–2]
В фундаментальном анализе широко известна следующая модель:
, (2)
где 
- это доходность акций компании,
— ожидаемый рост стоимости акций.
Предполагая, что ожидаемые перспективы роста стоимости акций равны нулю
= 0, получим следующее выражение для определения средней ожидаемой доходности:
(3)
-
Определение ожидаемой доходности акций
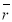на основе модели Гордона [8]
Модель Города [8] применяется для определения текущей стоимости актива (
), которая может быть найдена следующим образом:
(4)
где 
- размер дивидендных выплат в базисном году по отношению к планируемому периоду,
- это ожидаемая доходность акций компании,
— ожидаемый темп роста дивидендных выплат [8].
Соответственно, ожидаемая доходность акций может быть определена по формуле:
(5)
-
Определение ожидаемой доходности акций
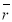через текущее и справедливое значение коэффициента 
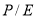с учетом вероятного горизонта инвестирования (3 года) [2].
Ожидаемая доходность акций может быть определена из выражения:
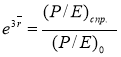, (6)
где 
- справедливое значение коэффициента 
, рассчитанное исходя из справедливой (внутренней) стоимости акций компаний,
— текущее значение коэффициента 
,
- это ожидаемая доходность акций компании.
Откуда, ожидаемая доходность акций компании:
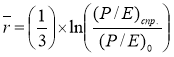(7)
В качестве исходных данных для оценки эффективности инвестиционного портфеля, сформированного по алгоритму Г. Марковица, модифицированного фундаментальными моделями доходности ценных бумаг на российском финансовом рынке выступали данные о ценах высоколиквидных акций российских компаний [10] за период 01.01.2014–01.01.2015 гг. Для диверсификации портфеля были выбраны акции семи компаний, представляющих разные отрасли экономики: ОAO «Лукойл», ОAO «Группа компаний ПИК», ОAO «Норильский Никель», ОAO «ВТБ», ОAO «Татнефть», ОAO «Росбанк», ОAO «Магнит» [10]. По данным фондовым активам рассчитывались ожидаемые доходности по формуле (1) и риск, а также коэффициент корреляции между ними.
Затем определялось достижимое и эффективное множество портфелей ценных бумаг в соответствии с классическим алгоритмом Г. Марковица [9]. Методика выбора оптимального портфеля основывалась на подходе Г. Марковица [9], дополненного идеями У. Шарпа [7]. Выбор оптимального портфеля осуществлялся графическим способом путем совмещения на одном графике эффективной границы Г. Марковица и линии, выходящей из точки безрисковой ставки, на которой располагаются портфели, включающие рискованные и безрисковые финансовые активы. Таким образом, были получены координаты (риск, доходность) оптимального портфеля и определен его состав. Так, было выяснено, что наиболее эффективным портфелем является портфель, на 90 % состоящий из акций ОAO «Группа компаний ПИК» и на 10 % — из акций ОАО «ВТБ». Инвестиционные характеристики — ожидаемая доходность и риск данного портфеля приведены в таблице 1.
Далее проводилась модификация подхода Г. Марковица [9] с помощью фундаментальных моделей доходностей. По исследуемым фондовым активам последовательно рассчитывалась их ожидаемая доходность по формулам (3), (5) и (7) и в соответствии с классическим алгоритмом Г. Марковица [9], описанным выше и дополненным идеями У. Шарпа [7], определялся оптимальный портфель ценных бумаг.
Инвестиционные характеристики полученных оптимальных портфелей представлены в таблице 1.
Таблица 1
Инвестиционные характеристики оптимальных портфелей, полученных при использовании алгоритма Г. Марковица, а также его модификаций с помощью фундаментальных моделей доходностей
|
Методика |
Ожидаемая доходность, (%) |
Риск, (%) |
|
Алгоритм Г. Марковица |
101,4 |
32,4 |
|
Алгоритм Г. Марковица, модифицированный фундаментальной моделью доходности, выраженной через текущее и справедливое значение коэффициента |
214,6 |
28,4 |
|
Алгоритм Г. Марковица, модифицированный фундаментальной моделью доходности, выраженной через коэффициент |
31,6 |
25,6 |
|
Алгоритм Г. Марковица, модифицированный фундаментальной моделью доходности Гордона (5) |
67,0 |
25,2 |
с учетом вероятного горизонта инвестирования (7)
(3)
Из таблицы 1 видно, что наиболее привлекательными инвестиционными характеристиками обладает оптимальный портфель, построенный с помощью алгоритма Г. Марковица, модифицированного моделью доходности, выраженной через текущее и справедливое значение коэффициента 
с учетом вероятного горизонта инвестирования. Применение данной модели позволяет достичь высокой доходности при низком уровне риска.
Вместе с тем, портфель ценных бумаг, отобранный по алгоритму Г. Марковица, также демонстрирует высокую эффективность.
Сопоставление представленных в таблице 1 инвестиционных характеристик оптимальных портфелей с их фактическими значениями показало, что именно указанные портфели (оптимальный портфель по Г. Марковицу и портфель, построенный с помощью алгоритма Г. Марковица, модифицированного моделью доходности, выраженной через текущее и справедливое значение коэффициента с учетом вероятного горизонта инвестирования) являются наиболее эффективными. Так, фактическая доходность портфеля, сформированного по алгоритму Г. Марковица, за исследуемый период времени составила 162 %, а портфеля, построенного по алгоритму Г. Марковица, модифицированного моделью доходности (7) была равна 68 % [10]. Ввиду того, что в модели (1.7) горизонт владения принимается равным три года, то предполагается, что ожидаемые инвестиционные характеристики, указанные в таблице 1, могут быть достигнуты в трехлетней перспективе.
Таким образом, на основе произведенных расчетов, можно сделать вывод о том, что наиболее эффективной методикой для построения оптимального портфеля является алгоритм Г. Марковица [9] и его модификация с помощью фундаментальной модели (7) [2].
Литература:
1.Брейли, Р. Принципы корпоративных финансов / Р. Брейли, С. Майерс; пер. с англ. Н. Н. Барышниковой. — М.: Олимп-бизнес, 2008. — 1008 с.
2.Грэхем Б., Додд Д. Анализ ценных бумаг / Б. Грэхем, Д. Додд; пер. с англ. — М.: Вильямс, 2015. — 880 с.
3.Кашина О. И. Об использовании анализа дивидендной доходности с целью совершенствования инвестиционных стратегий на финансовом рынке / О. И. Кашина // Молодой ученый. — 2014. — № 21 (80). — С. 332–335.
4.Некрасова, И. В. Определение степени эффективности российского фондового рынка на современном этапе функционирования / И. В. Некрасова // Вопросы регулирования экономики. — 2010. — Т. 1, № 2. — С. 5–16.
5.Петров С. С., Кашина О. И. О возможностях прогнозирования доходности финансовых активов на основе анализа биржевых котировок / С. С. Петров, О. И. Кашина // Аудит и финансовый анализ. — 2015. — № 2. — С. 135–140.
6.Петров С. С., Кашина О. И. Оптимизация активной стратегии управления портфелем ценных бумаг по критериям ожидаемой доходности и риска / Петров С. С., Кашина О. И. // Аудит и финансовый анализ. — 2013. — № 2. — С. 217–227.
7.Шарп У. и др. Инвестиции / Уильям Ф. Шарп, Гордон Дж. Александер, Джэффри В. Бэйли; пер. с англ. — М.: ИНФРА-М, 2001. — XII, 1028 с.
8.Gordon M. J. Dividends, Earnings, and Stock Prices / M. J. Gordon // The Review of Economics and Statistics. — 1959. — Vol. 41. — № 2, Part 1. — Р. 99–105.
9.Markowitz H. Portfolio selection / H. Markowitz // Journal of finance. — 1952. — Vol. 7. — No. 1. — P. 77–91.
10. Investfunds: информационное агентство [Электронный ресурс]: официальный сайт. Режим доступа: http://www.investfunds.ru/, свободный.
