В статье кратко изложены основы теории квантовых вычислений. Рассматриваются свойства кубитов, правила преобразования над ними, различные типы квантовых гейтов. Описан пример реализации квантового алгоритма Гровера в программе EXCEL. Показано преимущество квантового алгоритма Гровера над классическими алгоритмами.
Ключевые слова: квантовый компьютер, квантовый гейт, кубит, алгоритм Гровера.
Квантовая информатика на протяжении более двух десятков лет является одной из самых развивающих наук, поэтому создания квантового компьютера считается одним из наиболее актуальных идей в веке высоких технологий. Объясняется такой интерес двумя причинами: во-первых, квантовые вычисления предоставляют новые возможности для кодирования, обработки и передачи информации (увеличение быстродействия вычислений и возможность решать ряд вычислительных задач, недоступных классическому компьютер); во-вторых — это миниатюризация элементов интегральных схем классических компьютеров. Успехи современной компьютерной индустрии основаны на увеличении количества и уменьшении размера элементов микросхем [1, с.5]. Согласно закону Мура число транзисторов на один квадратный дюйм в микросхемах классических компьютеров увеличивается со временем по экспоненциальному закону, а именно удваивается каждые 18–24 месяца [2, с.7]. Одновременно с этим, число атомов, необходимых для предоставления одного бита информации, экспоненциально уменьшается со временем. Поэтому рано или поздно транзисторы будут столь малы, что каждый из них будет состоять из нескольких десятков атомов. В таком случае пренебрежение квантово-механическими эффектами в таких структурах станет недопустимым, а классическая логика, на которой построены современные компьютеры, перестанут функционировать. На этом этапе квантовая информатика должна открыть другой способ увеличения быстродействия компьютеров, основанный на использовании квантовых эффектов. По словам Р. Фейнмана такие квантовые компьютеры окажутся экспоненциально более быстрыми при моделировании квантово-механических систем, чем их классические аналоги. Совсем недавно было разработано несколько алгоритмов, осуществление которых на квантовом компьютере превращает проблемы экспоненциальной сложности в проблемы полиномиальной сложности [3, с.12]. Среди таких алгоритмов, в первую очередь, следует отметить алгоритм П. Шора, позволяющий факторизовать большие числа за полиномиальное время, и алгоритм Л. Гровера для поиска в неупорядоченной базе данных, показывающий квадратичный прирост быстродействия [5, с.18].
У квантового компьютера есть несколько принципиальных отличий от классического, но с практической точки зрения основными являются две: экспоненциальный рост объема памяти с ростом количества ячеек и способность за один такт работы обрабатывать всю имеющуюся в его распоряжении память. Иными словами, добавляя всего одну ячейку памяти, мы увеличиваем быстродействие квантового компьютера в два раза. Наибольшая надежда возлагается на квантовый параллелизм — возможность квантового регистра находиться одновременно во всех своих состояниях [4, с.35]. В основе квантового параллелизма лежит использование при вычислениях суперпозиций базисных состояний, что позволяет одновременно производить большое количество вычислений с различными исходными данными. Элементарным шагом при квантовых вычислениях является отдельная унитарная операция над N-кубитовой суперпозицией в квантовых компьютерах, тогда как для классического компьютера такая операция потребовала бы ![]() элементарных шагов. Например, 64-разрядный квантовый регистр может хранить до
элементарных шагов. Например, 64-разрядный квантовый регистр может хранить до![]() значений одновременно, а квантовый компьютер может все эти значения одновременно обрабатывать.
значений одновременно, а квантовый компьютер может все эти значения одновременно обрабатывать.
Основным понятием в информатике является бит. При измерении информация может принимать два значения 0 и 1. В классической ситуации под битом можно подразумевать переключатель с двумя четко различными состояниями. Квантовым аналогом бита выступает кубит (Q-бит, Quantum бит, квантовый бит), который представляет из себя квантово-механическую систему, обладающую двумя базисным состояниями: ![]() . В дираковской системе обозначений векторных величин используется разбиение английского слова bracket (скобка) на два слога: bra («бра») вектор — строки и ket («кет») вектор –столбцы. Запись кет — вектора выглядит как
. В дираковской системе обозначений векторных величин используется разбиение английского слова bracket (скобка) на два слога: bra («бра») вектор — строки и ket («кет») вектор –столбцы. Запись кет — вектора выглядит как ![]() , а бра — вектор записывается как
, а бра — вектор записывается как ![]() В обозначении внутреннего (скалярного) произведения два вектора оказываются заключенными в своеобразные скобки, например,
В обозначении внутреннего (скалярного) произведения два вектора оказываются заключенными в своеобразные скобки, например, ![]() . В общем случае, состояние такой системы задается волновой функцией вида:
. В общем случае, состояние такой системы задается волновой функцией вида:
![]() |
|![]() +
+ ![]() |
|![]() (1.1)
(1.1)
где α и ![]() — комплексные коэффициенты. При измерении состояния системы с волновой функцией, вероятность обнаружить ее в состоянии |
— комплексные коэффициенты. При измерении состояния системы с волновой функцией, вероятность обнаружить ее в состоянии |![]() равна
равна ![]() , а вероятность обнаружить ее в состоянии |
, а вероятность обнаружить ее в состоянии |![]() равна
равна ![]() . Сумма этих вероятностей равна единице:
. Сумма этих вероятностей равна единице:
![]()
![]() = 1 (1.2)
= 1 (1.2)
Выражение (1.1), записано в традиционной форме, характерной для квантовой механики «состояний».
В матричной форме бра-векторы принято обозначать следующим образом:
![]() (1 0),
(1 0), ![]() (0 1), (1.3)
(0 1), (1.3)
В матричной форме кет-векторы принято обозначать следующим образом:
|![]()
![]() , |
, |![]() , (1.4)
, (1.4)
Рассмотрим пример.
Имеется кубит в квантовом состоянии ![]() |
|![]() +
+ ![]() |
|![]() В этом случае, вероятность получить при измерении 0 составляет
В этом случае, вероятность получить при измерении 0 составляет ![]() = 49/81 = 60 %, вероятность получить при измерении 1 составляет
= 49/81 = 60 %, вероятность получить при измерении 1 составляет ![]() = 36/81 = 40 %. В данном случае, при измерении мы получим 0 с 60 % вероятностью. Как известно, в результате измерения кубит переходит в базисное состояние |
= 36/81 = 40 %. В данном случае, при измерении мы получим 0 с 60 % вероятностью. Как известно, в результате измерения кубит переходит в базисное состояние |![]() .
.
Пусть регистр состоит из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 базисных состояния: |![]() , |
, |![]() , |
, |![]() |
|![]()
Тогда квантовое состояние системы из двух кубитов имеет вид:
|![]() = a|
= a|![]() |
|![]() |
|![]() d |
d |![]() (1.5)
(1.5)
При измерении системы (1.5) вероятность обнаружить ее в состоянии |![]() равна
равна ![]() , |
, |![]() равна
равна ![]() |
|![]() равна
равна ![]() , |
, |![]() равна
равна ![]() . Отметим, что
. Отметим, что ![]() +
+ ![]() +
+ ![]() +
+ ![]() = 1 как полная вероятность [5,с.63].
= 1 как полная вероятность [5,с.63].
В матричном виде базисные состояния системы могут быть получены путем тензорного умножения однокубитных кэт-векторов:
|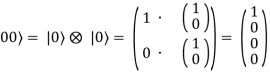 ; (1.6)
; (1.6)
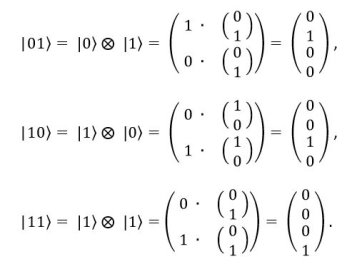
где ![]() знак тензорного умножения.
знак тензорного умножения.
С квантовыми системами можно производить только линейные унитарные преобразования, что эквивалентно поворотам вектора длиной 1 в трехмерном пространстве.
Рассмотрим основные элементарные преобразования. Их можно выполнить при помощи так называемых квантовых вентилей (квантовых гейтов) — умножением матричной формы кет-вектора на матричную форму вентиля [6, с.42].
Таблица 1
Квантовые вентили
|
Название, обозначение и краткое описание квантового вентиля |
Действие на базисные состояния |
Матричная форма вентиля |
|
Однокубитовые: |
||
|
Тождественное преобразование (I) |
|
| |
|
|
Отрицание (X или NOT) |
|
| |
|
|
Фазовый сдвиг (Z) |
|
| |
|
|
Фазовый сдвиг с отрицанием (Y) |
|
| |
|
|
Преобразование Уолша-Адамара (H) |
|
| |
|
|
Двухкубитовые: |
||
|
Управляемое отрицание (ControlledNOT или СNOT) |
|
|
|
| |
|
|
Трехкубитовые: |
||
|
ВентильТоффоли (ССNOT) |
|
|
|
|
|
|
|
| |
|
Важнейшим двухкубитовым оператором является CNOT, или управляемый NOT.
В базисе |![]() , |
, |![]() , |
, |![]() |
|![]() матрица оператора CNOT имеет вид:
матрица оператора CNOT имеет вид:
 (1.7)
(1.7)
Распишем действие этой матрицы на базисные векторы:

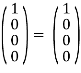 ,
, 
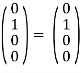 , (1.8)
, (1.8)

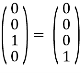 ,
, 
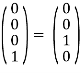 ,
,
Если первый кубит находится в состоянии ![]() , а второй кубит находится в одном из базисных состояний
, а второй кубит находится в одном из базисных состояний ![]() или
или ![]() , то под действием оператора CNOT состояние такой двухкубитовой системы не изменится. Если же первый кубит находится в состоянии
, то под действием оператора CNOT состояние такой двухкубитовой системы не изменится. Если же первый кубит находится в состоянии ![]() , а второй — в одном из базисных состояний, то оператор CNOT переводит второй кубит в другое базисное состояние. Состояние же первого кубита не изменится:
, а второй — в одном из базисных состояний, то оператор CNOT переводит второй кубит в другое базисное состояние. Состояние же первого кубита не изменится:
![]() (1.9)
(1.9)
![]() .
.
Оператор CNOT изображается в виде квантовой схемы:
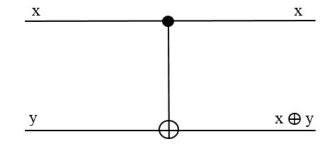
Рис. 1. Квантовая схема, изображающая оператор CNOT
Условно по двум проводам, слева направо, к схеме подводятся два кубита x и y. По двум правым проводам, от схемы отводятся два кубита — результат действия схемы [7, с.50]: неизменённый управляющий х, управляемый же у преобразуется в х
![]() (2.0)
(2.0)
Ниже в программе EXCEL представлены примеры действия оператора СNOT на некоторые векторы. Так, в примере 1 на входе имеем |![]() = 0.4 |
= 0.4 |![]() |
|![]() |
|![]() 0.2 |
0.2 |![]() :
:
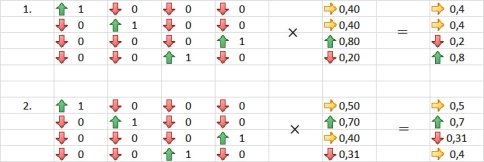
В результате получим вектор |![]() = 0.4 |
= 0.4 |![]() |
|![]() |
|![]() 0.8 |
0.8 |![]()
Квантовый алгоритм Гровера
Пусть имеется база данных, состоящей из ![]() записей. Одна из записей удовлетворяет некоторому заданному условию. Задача состоит в том, чтобы найти эту запись. Предполагается, что база данных представляет собой неупорядоченную, неструктурированную совокупность записей.
записей. Одна из записей удовлетворяет некоторому заданному условию. Задача состоит в том, чтобы найти эту запись. Предполагается, что база данных представляет собой неупорядоченную, неструктурированную совокупность записей.
В классическом случае поиск требуемой записи осуществляется методом полного перебора, по которому требуется проверить в среднем ![]() записей. В общем случае необходимо проверить О
записей. В общем случае необходимо проверить О![]() запись, где О (…) обозначает термин «не более чем».
запись, где О (…) обозначает термин «не более чем».
Например, рассмотрим неупорядоченную базу данных, содержащую 1024 записей. Мы хотим найти ровно одну запись. Для того чтобы решить эту задачу на обычном компьютере, в худшем случае, нам придется перебрать все 1024записей, а в среднем 512 — это очевидно. На квантовом компьютере необходимо и достаточно произвести 25 итераций, чтобы найти данную запись. Для 16 384 записей в классическом среднем случае придется перебрать 8 192 записи. На квантовом компьютере необходимо и достаточно произвести 100 итераций.
В общем случае алгоритм Гровера (рис.2) позволяет выполнить поиск требуемой записи за ![]() шагов.
шагов.
Задачу поиска в неупорядоченной базе данных можно сформулировать следующим образом.
Задана неупорядоченная совокупность элементов
![]()
Требуется найти «маркированный» элемент ![]() .
.
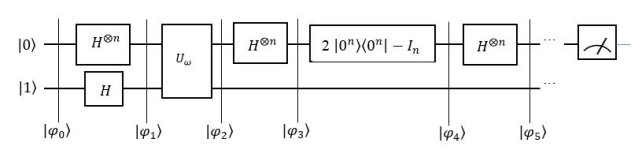
Рис. 2.Квантовый двухкубитный алгоритм Гровера.
Рассмотрим пример. Пусть база данных содержит 4 записи. В худшем случае, нам придется перебрать все 4записи, а в среднем 2. На квантовом компьютере достаточно произвести 1 итерацию, чтобы найти данную запись.
Алгоритм включает в себя следующие шаги.
-
Приготовление начального состояния квантового регистра, состоящего из
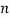 кубитов. Каждый кубит устанавливается в состояние |
кубитов. Каждый кубит устанавливается в состояние |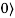 . Состояние регистра запишем вектор в виде:
. Состояние регистра запишем вектор в виде:
![]() (2.2)
(2.2)

- Приготовление равновероятной (с равными амплитудами) суперпозиции состояний кубитов с помощью преобразования Уолша — Адамара:

-
Поворот амплитуды «маркированного» состояния
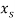 . Для этого необходимо выполнить преобразование:
. Для этого необходимо выполнить преобразование:
![]()

- Преобразование Адамара:

- Вычисление инверсии относительно среднего:

-
Преобразование Адамара (возвращает в начальное состояние
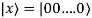 ):
):

Таким образом, выполнив одну итерацию мы нашли функцию, которая принимает значение 1 только на одном из 4-х вариантов входных значений. Следовательно, процедура поиска заметно ускорилась теоретически на ![]() по сравнению с расчетами на классическом компьютере.
по сравнению с расчетами на классическом компьютере.
Очевидно, что классические компьютеры и алгоритмы в ближайшее время достигнут максимальной производительности. Поэтому необходимо разрабатывать новые алгоритмы и программы для квантовых компьютеров уже сегодня.
Литература:
- Валиев К. А. Квантовые компьютеры: надежды и реальность // К. А. Валиев, А. А. Кокин — Ижевск; РХД, 2001. — 352 с.
- Quantum algorithms revisited / R. Clever, A. Ekert, C. Mosca // Proc.Roy. Soc. Lond. A. — 1998. — Vol. 454. Pp. 339–354.
- Galindo A. Information and computation: classical and quantum aspect / A.. Galindo, M. A. Martin — Delgado // Reviews of Modern Physics. — 2002. — Vol. 74, no. 2. — Pp. 347–423.
- Международный научный журнал: «Квантовые компьютеры и квантовые вычисления», № 1,2000.
- Чивилихин С. А. Учебное пособие «Квантовая информатика». 2009.
- Cадовничий В. А. Квантовые компьютеры и квантовые вычисления. № 2
- Хренников А. Ю. Введение в квантовую теорию информации. 2008.









