Разработки в сфере распознавателей объектов являются одними из приоритетных в робототехнике. Существующие методы определения типа дорожного покрытия работают в условиях непосредственного физического контакта с определяемой поверхностью. Разработка метода определения типа дорожного покрытия на расстоянии позволит системам ориентирования и системам устойчивости работать в реальных городских условиях. Практическая значимость бесконтактного метода определения типа дорожного покрытия позволит беспилотным устройствам и системам устойчивости работать с более высокой скоростью, без риска потери маршрута устройством ([1, с. 25]).
Структурная схема разрабатываемой системы. Бесконтактная, ультразвуковая система распознавания дорожного покрытия (рис. 1) работает следующим образом. Информация с датчиков необходимых для определения коэффициента сцепления в данный момент поступает с датчиков в анализатор, затем в БУ. Параллельно с этим БУ получает данные с датчиков необходимых для прогнозирования дорожной ситуации.
Рис. 1. Структурная схема бесконтактной системы определения дорожного покрытия
Определив моментальные значения коэффициента сцепления, и показания портативной метеостанции, система корректирует показания с ультразвуковых датчиков и инфракрасных датчиков, на основе имеющихся в ней данных и окружающих погодных условий. Закончив корректировку, система производит проверку корректировки (когда транспортное средство достигает места прогнозируемой дорожной ситуации система сверяет данные о моментальной ситуации с прогнозированными данными).Далее тип дорожного покрытия идентифицируется системой, либо тип дорожного покрытия для системы является неизвестным. Система, используя встроенные базы данных продолжает прогнозирование дорожного покрытия и посылает сигнал о прогнозируемой ситуации на выходы.
Модель покоординатного перемещения контактной части автомобиля.
Метод покоординатного контроля поверхности основан на бесконтактном способе определения микро профиля контактной поверхности и наклона дорожного покрытия описываемого дифференциальными уравнениями, и СЛАУ координатного перемещения контактной части автомобиля. Определение реакции опоры при неравномерной нагрузке производится путём установления датчиков давления, измеряющих массу давления (m) на каждый из амортизаторов (рис. 2) автомобиля и установки датчиков расстояния внутри амортизаторов. Датчики расстояния измеряют расстояния от верхней точки пружины амортизатора до нижней (u).
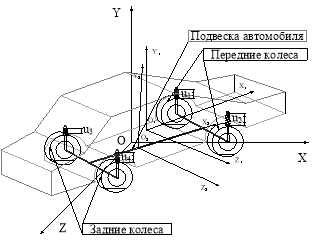
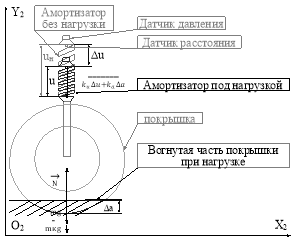
Рис. 2. Схематичное изображение измеряемых величин
Имея данные с датчиков становится возможным рассчитать такие величины как: прогиб покрышки (∆a), прогиб амортизатора (∆u), реакция опоры (N) каждого колеса в отдельности. Автомобиль представляет из себя систему из двух подвижных частей, связанных амортизаторами, а именно подвески и корпуса.
Для удобства решено присвоить каждой из этих частей по системе координат, что позволит наглядно показать принцип работы системы подвески и качественно строить проекции, основываясь на углах смещения осей координат
На рисунке 1 к автомобилю привязаны 2 плоскости, (O1, X1, Y1) — к центру масс корпуса, так, что ось ОX1 привязана к центральной линии корпуса по горизонтали продольно, а ось OY1 — привязана к её перпендикуляру по вертикали. Плоскость (O2, X2, Y2) — к центру масс подвески. Ось OY привязана к вектору силы земного притяжения.
Учитывая тот факт, что в нашем данном случае векторы сил совпадают с вектором (→ ┬ Y), для удобства можно брать значения сил по модулю.
Реакция опоры равна силе воздействия на нее
Где (→ ┬ N) — вектор реакции опоры, (→ ┬ g) — притяжение земли, m — масса действующая на амортизатор mк — масса колеса и части подвески.
│mg+ mкg│= ku∆u + ka∆a
Где ku — коэффициент упругости пружины амортизатора, ka — коэффициент упругости накаченной покрышки (значения берутся табличные либо экспериментальные)
∆u = (│mg+ mкg│– ka∆a)/ku
Прогиб амортизатора рассчитывается путем нахождения разницы между нормальной длиной пружины амортизатора (uн) и измеренной длиной пружины амортизатора
∆u = uн — u
∆a = (│mg + mкg│– ku∆u)/ka; ∆a = (│mg + mкg│– ku(uн-u)/ka
Масса колеса — величина постоянная, а вот масса подвески будет меняться в зависимости от угла наклона автомобиля и скорости центростремительного ускорения (в случае центростремительного движения)
Где mкол — масса колеса, mп — воздействующая на колесо часть массы подвески
Проверку расчетов возможно произвести по массе корпуса (mo)
mi = (∆aika + ku(uн + ui)/g — mкi
Масса всего корпуса распределятся между четырьмя соединительных точках, в которых измеряется масса при предлагаемом методе.
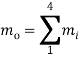или mo = m1 + m2 + m3 + m4
Сложив нагрузку на каждый амортизатор в отдельности можно получить вес всей верхней части автомобиля.
mo= 
+
+
+
Вывод: Зная давление на каждом амортизаторе и зная степень сжатия амортизатора можно получить такие величины как: прогиб покрышки, прогиб амортизатора, реакция опоры каждого колеса в отдельности. Это позволит управлять жёсткостью подвески в зависимости от неровностей дороги.
Результаты математического моделирования. Важной характеристикой типа дорожного покрытия является микро профиль [2, с. 145]. Для определения величины микро профиля необходимо рассчитать такие величины как момент на ведущем колесе и радиальную нагрузку на колесо (рис 3). Момент на ведущем колесе Mк измеряется в соотношении между его величиной, радиальной нагрузкой на колесо Gк, коэффициентом сопротивления качению f0 и радиусом качения колеса в ведомом состоянии rк:
Mк = rкf0Gк.
Радиальная нагрузка на колесо использует уравнение равновесия сил, возникающих в контакте колеса с дорогой:
Mg + mg + 2cш(hсг(t) (t)) = Gк(t).
Расчет высоты микро профиля под ведущим колесом, и как следствие, прогиба шины hсг(t) (t), приводит к необходимости определения случайной переменной составляющей усилия в контакте колеса с дорогой:
Gк(t) = 2cш(hсг(t) (t)).
Микро профиль дороги представляется в виде стационарного эргодического случайного процесса с автокорреляционной функцией вида:
Rk() Dk (A1ke 1k cosk + A2ke),
где 1k, 2k, k — коэффициенты, найденные для k-го вида профиля, Dk — дисперсия k-го вида профиля (рис 3).
На основании усредненных измерений, выборочно проведенных на следующих типах грунта Ростовской области, были приведены коэффициенты аппроксимации автокорреляционной функции основных видов микро профиля (таблица 1).
Таблица 1
Коэффициенты аппроксимации автокорреляционной функции.
|
Тип дорожного покрытия |
Коэффициенты аппроксимации |
|||||
|
D,см2 |
A1 |
A2 |
1 |
2 |
|
|
|
Асфальт новый (R1) |
0,66 |
1 |
0 |
0,13 |
0 |
1,05 |
|
Асфальт изношенный (R2) |
1,6 |
0,15 |
0,85 |
0,05 |
0,2 |
0,6 |
|
Щебеночный (R3) |
6,3 |
0,05 |
0,95 |
0,05 |
0,21 |
1,37 |
|
Накатанный грунт (R) |
10,63 |
0,1 |
0,9 |
0,2 |
0,7 |
1,57 |
Замеры характеристик дорожного покрытия типа асфальт новый, проводились на трассе международного уровня А-280 с момента укладки до момента замеров прошло 3 месяца.
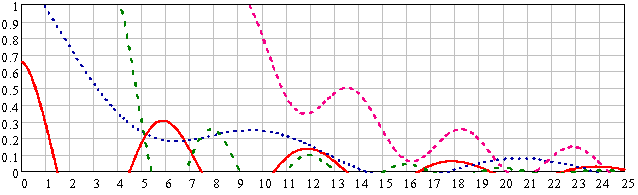
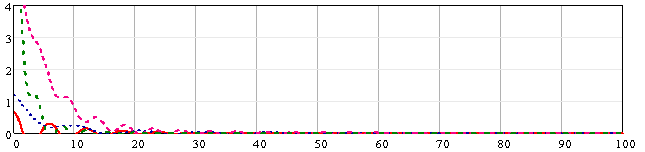Рис. 3. Автокорреляционные функции микро профиля дорожной поверхности
Таким образом исходный профиль, описываемый уравнением автокорреляционной функции вида Rk() Dk(A1ke 1kcosk + A2ke) (рис 3) где, R1 — асфальт новый, R2 — асфальт изношенный, R3 — Щебеночный, R4 — накатанный грунт, переменные взяты из таблицы 1.
Заключение. Предложена структурная схема системы ультразвукового распознавания дорожного покрытия, основанная на бесконтактной диагностике. Разработана модель покоординатного перемещения контактной части автомобиля. Предложен покоординатный метод определения микро профиля дорожного покрытия во время движения автомобиля, посредством ультразвука. Рассмотрен принцип работы метода и обоснован его практический смысл. Приведена математическая модель расчетов микро профиля дорожного покрытия. Исследованы характеристики различных типов микро профиля дорожного покрытия.
Литература:
- Пшихопов В. Х., Медведев М. Ю. Оценивание и управление в сложных динамических системах. — М.: Физматлит, 2009.
- Щуровский В. А. Математическое моделирование системы безопасного управления автомобилем в повороте // Инновации в сфере жизнедеятельности человека XXI века», Ростов-н/Д Изд-во Юнеско. 2015.
