Территория России характеризуется разветвленной газотранспортной сетью (рис.1). Эти магистрали являются источниками повышенной опасности, как с точки зрения экологии, так и возможного создания чрезвычайной ситуации при возникновении аварий на газопроводах. Предвестниками таких опасностей могут являться утечки газа, возникающие из-за механических повреждений трубопровода или его коррозии. Исходя из этого, раннее обнаружение утечек является актуальной задачей. Настоящая работа посвящена разработке инструментального метода обнаружения утечек газа из трубопроводов, который бы решал одну из основных проблем диагностики их состояния.
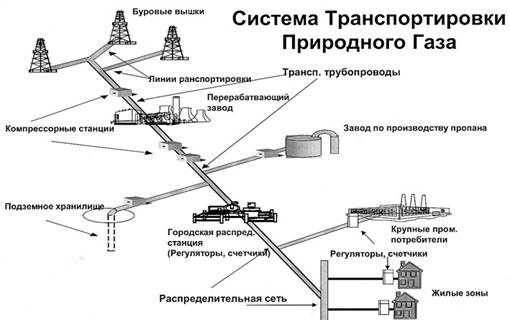
Рис. 1. Разветвленная система транспортировки газа от добычи до потребителя.
Анализ последних исследований и публикаций.
Основным методом обнаружения мест утечек в настоящее время является патрулирование газопроводов с применением переносных газоанализаторов. Этот метод связан с большими трудозатратами и отличается невысокой оперативностью. Более оперативными и перспективными представляются методы обнаружения утечек, основанные на анализе тепловых изображений земной поверхности в районе залегания трубопроводов [1,2], тепловизорами установленными на беспилотных летательных аппаратах. Принцип тепловизионной диагностики состоит в сравнении эталонного и анализируемого полей температуры. Аномалии температуры служат индикаторами дефектов, а величина температурных сигналов и их поведение во времени лежат в основе оценок параметров объектов. Над диагностируемой трассой запускают беспилотный летательный аппарат, оборудованный системой, состоящей из видеокамеры, тепловизора и системы спутниковой навигации. Беспилотный летательный аппарат, перемещаясь по заданному маршруту, осуществляет запись и передачу на Землю цифровой диагностической информации в виде последовательности привязанных к карте изображений. Стационарный комплекс на Земле в режиме реального времени осуществляет сшивку изображений в ленту, а также обработку и анализ полученной цифровой информации с целью выявления мест разрывов и утечек.
Постановка задачи и ее решение.
Метод основан на обнаружении тепловых аномалий на поверхности почвы, вызываемых резким перепадом давления газа при выходе из канала утечки и появлением локальных тепловых градиентов в слое почвы над трубопроводом. Рассмотрим задачу оценки влияния этого процесса на тепловое поле в грунте.
Для систем теплоснабжения, паропроводов и газопроводов трубопроводы, чаще всего, заложены в грунте – массиве. Объем неограниченного массива имеет коэффициент теплопроводности 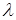 и бесконечные размеры по всем направлениям. Трубопроводы можно рассматривать как действующие сосредоточенные линейные, положительные и отрицательные источники теплоты длиною
и бесконечные размеры по всем направлениям. Трубопроводы можно рассматривать как действующие сосредоточенные линейные, положительные и отрицательные источники теплоты длиною 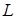 (рис. 2)
(рис. 2)
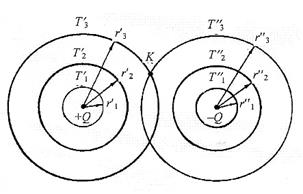
Рис. 2. Расположение источника и стока теплоты: 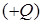 – положительные источники теплоты,
– положительные источники теплоты, 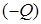 – отрицательные «стоки» теплоты,
– отрицательные «стоки» теплоты, 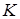 – место совмещения изотерм
– место совмещения изотерм
По сравнению с протяженностью 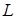 неограниченного массива источник
неограниченного массива источник 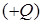 и «сток»
и «сток» 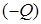 расположены близко друг к другу и поэтому путь между ними является линией наименьшего термического сопротивления. В связи с этим вся теплота, выделяемая источником, будет полностью поглощаться «стоком». Если бы источник и «сток» не воздействовали друг на друга, то каждый из них создавал бы в теле массива температурное поле в виде концентрических изотерм. Тогда
расположены близко друг к другу и поэтому путь между ними является линией наименьшего термического сопротивления. В связи с этим вся теплота, выделяемая источником, будет полностью поглощаться «стоком». Если бы источник и «сток» не воздействовали друг на друга, то каждый из них создавал бы в теле массива температурное поле в виде концентрических изотерм. Тогда
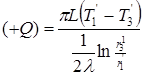 ;
; 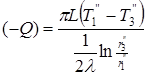 , откуда
, откуда 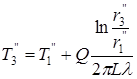
Если бы температурное поле в массиве формировалось только источником или только «стоком», то в точке 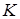 была бы температура
была бы температура 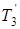 или же
или же 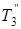 . При одновременном действии источников и «стоков» результирующее температурное поле получается путем сложения температурных полей, возбуждаемых в массиве отдельными источниками и «стоками» в предположении, что они не мешают друг другу. Если обозначить температуру источника теплоты через
. При одновременном действии источников и «стоков» результирующее температурное поле получается путем сложения температурных полей, возбуждаемых в массиве отдельными источниками и «стоками» в предположении, что они не мешают друг другу. Если обозначить температуру источника теплоты через 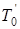 , а «стока» –
, а «стока» – 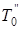 , то действительная температура в точке
, то действительная температура в точке 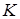 определится из выражения
определится из выражения
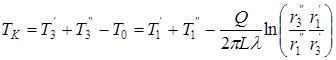
Для расчетов условно полагают, что теплота от цилиндрического газопровода 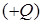 , заложенного в грунт, передается не в окружающую среду, а забирается отрицательным источником теплоты
, заложенного в грунт, передается не в окружающую среду, а забирается отрицательным источником теплоты 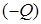 (рис.3).
(рис.3).
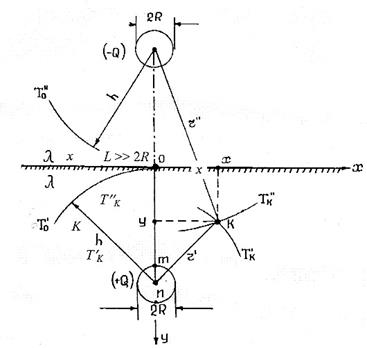
Рис. 3. Расположение газопровода. 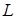 – длина цилиндра радиуса
– длина цилиндра радиуса 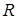 ;
; 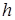 – глубина заложения;
– глубина заложения; 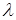 – коэффициент теплопроводности массива;
– коэффициент теплопроводности массива; 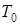 – температура поверхности слоя.
– температура поверхности слоя.
В этом случае «сток» 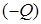 размещен симметрично источника
размещен симметрично источника 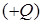 и окружен точно таким же массивом, а реальная картина температурного поля в грунте при этом не нарушается. Учитывая, что
и окружен точно таким же массивом, а реальная картина температурного поля в грунте при этом не нарушается. Учитывая, что
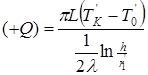 ;
; 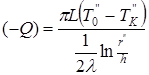
и используя принцип совмещения температурных полей, можно выразить температуры в любой точке 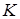 грунта:
грунта:
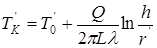 ;
; 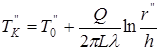
Суммируя температуры 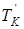 и
и 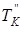 , получим:
, получим:
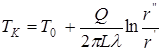 ,
,
или 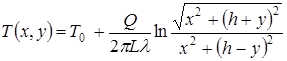 ,
,
Таким образом, температурное поле в грунте становится определенным, если замерена температура на поверхности массива 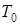 и известен поток теплоты
и известен поток теплоты 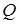 . С другой стороны, тепловой поток цилиндром может быть рассчитан по температуре поверхности массива и еще по одной, любой, температуре в грунте.
. С другой стороны, тепловой поток цилиндром может быть рассчитан по температуре поверхности массива и еще по одной, любой, температуре в грунте.
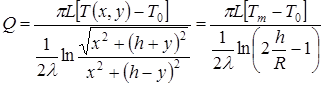
Естественно ожидать, что максимальная температура грунта будет в точке 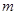 (
(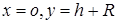 ) равна
) равна
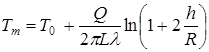
Если в массиве будет заложено два теплопровода, то соответственно им появляется и два стока. Температурное поле в грунте получится уже как результат совмещения четырех температурных полей.
Расчет температурного поля методом релаксации.
Релаксация – процесс установления термодинамического равновесия или восстановления неустойчивого положения в физической системе. Метод релаксации используется для решения задач стационарной теплопроводности в телах сложной конфигурации, когда при расчете температурного поля дифференциальное уравнение теплопроводности не поддается аналитическому решению.
Расчет температурного поля методом релаксации удобно иллюстрировать на примере, когда теплота распространяется в двух измерениях. Сечение тела (рис. 4 и 5) обычно разбивается релаксационной решеткой на ячейки квадратной формы 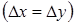 . Тело имеет глубину
. Тело имеет глубину 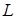 и коэффициент теплопроводности
и коэффициент теплопроводности 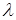 .
.
В дальнейшем допускается следующее:
1) процесс теплопроводности концентрируется в стержнях релаксационной решетки, и чем меньше будут размеры ячейки, тем выше точность вычислений, но количество расчетов при этом увеличится;
2) по каждому стержню релаксационной решетки передается в точности такое же количество теплоты, которое в действительности передается через элемент с размерами 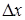 и
и 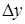 ;
;
3) в качестве расчетного соотношения может быть использована формула расчета теплого потока через плоскую стенку: 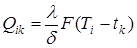 , где
, где 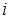 – отмечает наибольшее значение температуры;
– отмечает наибольшее значение температуры; 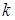 – отмечает наименьшее значение температуры.
– отмечает наименьшее значение температуры.
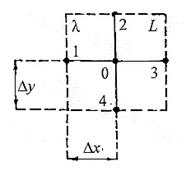
Рис. 4. Ячейка релаксационной решетки
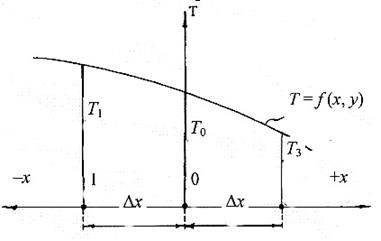
Рис. 5. Проекция ячейки релаксации
Приняв эти допущения, можно рассчитать количество теплоты, которое протекает по каждому стержню:
• для горизонтального стержня 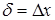 ,
, 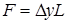
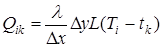
• для вертикального стержня 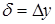 ,
, 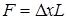
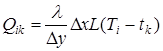
• для любого стержня
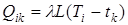 (1)
(1)
При этом могут иметь место различные схемы подвода и прохождения теплоты через ячейку релаксации.
1. Теплота идет от точки 1 к узловой точке 0, а от точки 0 расходится в направлении точек 2, 3, 4. Уравнение баланса теплоты имеет вид 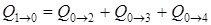 . Согласно (1)
. Согласно (1)
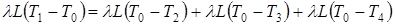
откуда 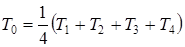
2. Теплота идет от точек 1 и 2 к точке 0, а от точки 0 расходится к точкам 3 и 4. Уравнение баланса имеет вид 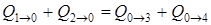 , или
, или
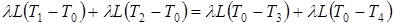
откуда 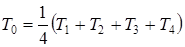
3. Теплота идет от точек 1,2,3,4 к точке 0 и там взаимно уничтожается. Уравнение баланса тепла имеет вид 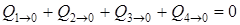 , или
, или
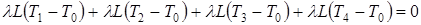 ,
,
откуда 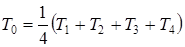 .
.
Следовательно, какова бы ни была схема прохождения теплоты, температура в узловой точке квадратной релаксационной ячейки всегда будет равна среднему арифметическому значению из температур, окружающих эту точку.
Для каждой узловой точки релаксационной решетки существует закон релаксации:
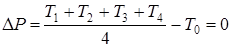 (2)
(2)
Принцип релаксации заключается в следующем:
1. Тело сложной конфигурации разбивается на релаксационную решетку. Исходя из предварительного объема знаний, приближенно задают значения температур в узлах решетки.
2. Эти приближения проверяются от точки к точке в соответствии с требованием закона релаксации и устанавливают точки, в которых наблюдается наибольшее отклонение от закона релаксации (2).
3. Начиная с мест (точек) наибольшего отклонения, вносятся поправки 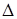 , чтобы удовлетворить закону релаксации.
, чтобы удовлетворить закону релаксации.
4. Эти исправления в свою очередь вызывают новые отклонения в соседних точках решетки, и возникает необходимость в повторной коррекции.
5. Повторная коррекция вносится каждый раз последовательно в порядке убывающих отклонений и производится до тех пор, пока численные значения температур во всех точках сетки не придут во взаимное соответствие, т.е. везде будет соблюдаться закон релаксации.
Записав уравнение (2) для каждого из узлов тепловой сетки, получим систему, состоящую из числа линейных уравнений, равного числу узлов сетки. Для решения этой системы уравнений применяют различные численные методы, и в частности, метод релаксации. Название метода происходит от латинского “relaxation” - ослабление, означающего постепенный переход системы в равновесное состояние. Например, если температура в каком-либо узле сетки, зависящая от четырех соседних значений температуры, находится в равновесии с ними, то выполняется уравнение (2). Если она не находится в равновесии с соседними значениями температуры, то правая часть этого уравнения не будет равна нулю, т.е.
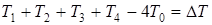 (3)
(3)
где 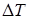 - остаток.
- остаток.
Для сведения к нулю правой части (остатка) каждого из уравнений системы, т.е. для приведения системы в равновесное состояние, и применяется этот метод.
Как уже написано выше, глубинный профиль температуры в грунте, связанный процессами солнечного нагрева почвы и теплообмена поверхности с окружающей средой может быть рассчитан в соответствии с законом Фурье [4].
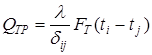 , (4)
, (4)
где 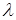 - коэффициент теплопроводности грунта;
- коэффициент теплопроводности грунта; 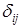 - расстояние между точками
- расстояние между точками 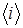 и
и 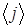 ;
; 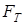 - площадь теплообмена;
- площадь теплообмена; 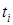 ,
, 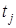 - температуры грунта в точках
- температуры грунта в точках 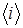 и
и 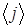 , соответственно.
, соответственно.
Наличие в деятельном слое грунта трубопровода приводит к нарушениям процесса теплопередачи [5] и вызывает искажения глубинного профиля этих изотерм. Этот процесс усиливается при отличии температуры газа в трубе от температуры грунта, что характерно для реальных условий прокачки газа при его транспортировке.
Для определения поля температур использован метод релаксаций. Для этого расчетная область с учетом симметрии относительно вертикальной оси, проходящей через цент трубы, разбивается сеткой на элементарные объемы. Для выбранной точки каждого объема составляется уравнение баланса тепла, позволяющее определить значение температуры.
Количество тепла, передаваемого от газа, движущегося в трубе, к грунту определялось по формуле
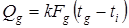 (5)
(5)
где 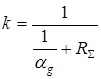 - коэффициент теплоотдачи;
- коэффициент теплоотдачи; 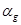 - коэффициент теплоотдачи от газа к стенкам трубопровода;
- коэффициент теплоотдачи от газа к стенкам трубопровода; 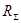 - суммарное термическое сопротивление стенки трубопровода и участка грунта между внешней поверхностью трубы и расчетной точкой
- суммарное термическое сопротивление стенки трубопровода и участка грунта между внешней поверхностью трубы и расчетной точкой 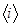 в грунте;
в грунте; 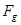 - теплоотдающая поверхность трубопровода;
- теплоотдающая поверхность трубопровода; 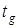 ,
,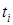 - температуры движущегося по трубопроводу газа и точки
- температуры движущегося по трубопроводу газа и точки 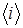 грунта, соответственно.
грунта, соответственно.
При возникновении утечки из газопровода массовая скорость истечения газа определяется отношением атмосферного давления и давления в трубе
Так, если перепад давлений атмосферного воздуха 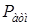 (Па) и давления в газопроводе
(Па) и давления в газопроводе 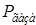 (Па) удовлетворяет неравенству:
(Па) удовлетворяет неравенству:
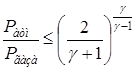 ,
,
то в начальный момент времени истечение газа происходит со звуковой скоростью (такой режим наблюдается в случае перекачки газа под давлением более 0,18 МПа). Здесь γ=ср/сν - отношение теплоемкостей.
Массовая скорость звукового истечения газа определяется как:
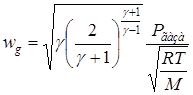 , кг/с
, кг/с
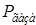 – давление в трубопроводе (Па),
– давление в трубопроводе (Па),
Т – температура в газопроводе (К),
R = 8314 – универсальная газовая постоянная (кг∙м2/К∙кмоль∙с2),
М – молярная масса (кг/кмоль).
Чем больше перепад давления, тем больше скорость и массовый расход газа при истечении и скорость истечения становится равной так называемой критической скорости, равной местной скорости звука
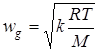
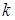 - величина показателя адиабаты газа.
- величина показателя адиабаты газа.
Для газа в модельном случае возьмем метан с 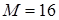 , примем
, примем 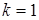 и тогда
и тогда 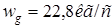
Расход 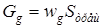
где 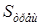 – площадь трещины в газопроводе (м2).
– площадь трещины в газопроводе (м2).
Количество тепла, отводимого выходящим через отверстие газом, может быть определено, согласно [3], по формуле
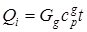 (6)
(6)
где, 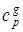 - удельная теплоемкость газа Дж/(кг*К).;
- удельная теплоемкость газа Дж/(кг*К).; 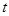 - температура газа (К).
- температура газа (К).
Утечка в расчетах имитировалась стоком тепла, помещенным в точку 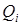 (см. рис.7). Интенсивность стока из отверстия размерами (1х0,1) мм2 в соответствии с [3] оценена, как
(см. рис.7). Интенсивность стока из отверстия размерами (1х0,1) мм2 в соответствии с [3] оценена, как 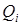 = -33,15 Вт для температуры газа + 240С и давления в трубе 70 атм.
= -33,15 Вт для температуры газа + 240С и давления в трубе 70 атм.
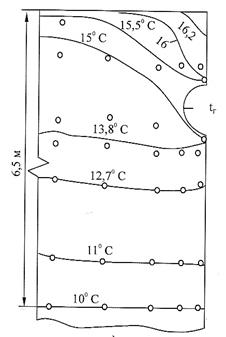
Коэффициент теплопроводности грунта в расчетах принимался равным 1,49 Вт٠м-1 ٠град-1. Температура воздуха в расчетах принималась равной 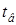 = 200С. Рассчитанные изотермы приведены на рис.6 и рис.7 кружками.
= 200С. Рассчитанные изотермы приведены на рис.6 и рис.7 кружками.
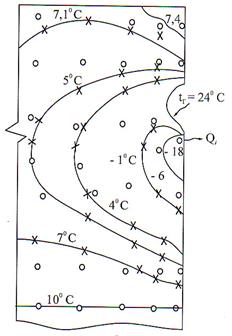
На рис.7 приведены расчетные изотермы для утечки, расположенной в нижней части трубы. Расположение стока тепла в верхней части увеличит «тепловой провал», соответствующий месту утечки. Пространственное распределение теплового поля на поверхности может быть получено путем вращения рисунка 7 вокруг оси, проходящей через центр трубопровода.
|
Рис.6. Распределение поля температур в грунте при нормальном состоянии газопровода |
Рис.7. Распределение поля температур в грунте при наличии утечки в газопроводе |
Выводы.
Оценки вероятности обнаружения, проведенные по методике, представленной в [5] для беспилотных летательных аппаратов с ИК аппаратурой (например GasFindIR), показывают возможность правильной идентификации утечек с высот, характерных для патрульных полетов (200-500)м. С помощью разработанного комплекса программ были рассчитаны типичные варианты возможных повреждений газопроводов. Полученные выводы на основе анализа численных расчетов и атлас тепловых полей могут быть использованы при проведении реальных тепловизионных съемок трубопроводов.
ЛИТЕРАТУРА
1. Викторов В.А., Лункин Б.В., Совлуков А.С. Радиоволновые измерения параметров технологических процессов. М.: Энергоатомиздат, 1989. 208 с.
2. Неразрушающий контроль. Россия 1990.2000 гг.: справочник / под ред. В.В. Клюева и др. М.: Машиностроение, 2001. 203с.
3. Вулис Л.А. Термодинамика газовых потоков. М. . Л.: ГЭИ, 1950. 304 с.
4. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. М.-Л.:«Энергия»,1965. 424с.
5. Павлов Н.И., Эльц Е.Э. Обнаружение температурных аномалий, обусловленных заглубленными в грунт инородными объектами // Изв. ВУЗов. Радиоэлектроника». 2007. т.50, № 3. С.12-20.
6. Фокин В.М., Бойков Г.П., Видин Ю.В.//Основы энергосбережения в вопросах теплообмена. М.: «Издательство Машиностроение», 2005.192 с.