Имеется объект, описываемый линейным дифференциальным уравнением. Устройство управления этим объектом представляет собой параметрический регулятор (П-, ПИ-, ПИД-регулятор). Объект управления и управляющее устройство образуют замкнутую линейную динамическую систему с единичной отрицательной обратной связью – макрообъект (рисунок 1).
 |
|||
 |
 |
||


 |
Рис. 1 Схема замкнутой системы управления
На рисунке приняты следующие обозначения: x(t) – выход объекта, u(t) – вход объекта, 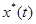 - задающее воздействие,
- задающее воздействие, 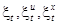 - помехи, действующие на объект и в каналах измерения.
- помехи, действующие на объект и в каналах измерения.
Ставится задача построения модели замкнутой ЛДС (макрообъекта) в случае малой априорной информации (имеются выборочные данные входных, выходных переменных, данные о структуре исследуемой системы отсутствуют). Предполагается возможность постановки эксперимента. В каналах измерения действует центрированная помеха с ограниченной дисперсией (что весьма часто встречается на практике и, таким образом, не идеализирует решаемую задачу).
Остановимся подробнее на управляющем устройстве. Как было указано ранее, в качестве такого устройства в данном случае выступает параметрический регулятор. Регуляторы в подавляющем большинстве работают по принципу отрицательной обратной связи с целью компенсировать внешние возмущения, действующие на объект управления, и обработать заданный извне или заложенный в системе закон управления.
Пропорционально-интегрально-дифференциальный регулятор, используемый в данной работе, – устройство в цепи обратной связи, используемое в системах автоматического управления для поддержания заданного значения измеряемого параметра. ПИД-регулятор измеряет отклонение стабилизируемой величины от заданного значения (задающего воздействия) и выдает управляющий сигнал, являющийся суммой трех слагаемых, первое из которых пропорционально этому отклонению, второе пропорционально интегралу отклонения и третье пропорционально производной отклонения (производной измеряемой величины).
Таким образом, выходной сигнал регулятора определяется тремя слагаемыми [5]:
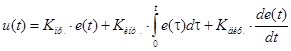 , (1)
, (1)
где Kпр, Kинт, Kдиф – коэффициенты усиления соответствующих составляющих регулятора, e(t) – невязка между выходом объекта и задающим воздействием (рассогласование).
Настройка аналогового регулятора сводится к настройке его параметров, которая может быть произведена согласно критериям устойчивости Гурвица и Михайлова при наличии явного вида передаточных функций объекта и корректирующих звеньев. В связи с тем, что на практике структура объекта управления неизвестна, настройка параметров аналоговых регуляторов производится эмпирически, что представляет определенную сложность, а также требует временных и финансовых затрат.
Не меньшую сложность представляет задача построения модели замкнутой системы. При отсутствии каких-либо сведений о структуре объекта управления построение параметрической модели весьма проблематично. При включении корректирующего устройства и замыкании отрицательной обратной связью структура исследуемой системы становится сложнее структуры объекта управления, что в свою очередь увеличивает число определяемых параметров, а значит и сложность параметрического моделирования. Усложнение структуры можно продемонстрировать, используя структурную схему замкнутой системы, позволяющую получить передаточную функцию замкнутой системы по имеющимся передаточным функциям входящих в нее звеньев [5]. Структурная схема замкнутой системы показана на рисунке 2.

Рис. 2 Структурная схема системы с отрицательной обратной связью
Рассмотрим случай использования ПИД-регулятора (рисунок 3), подключение которого (с учетом условия реализуемости технического устройства) приводит к дифференциальному уравнению замкнутой системы, на два порядка большему дифференциального уравнения объекта управления.

Рис. 3 Структурная схема ПИД-регулятора
Условием реализуемости технического устройства является следующее требование в передаточной функции 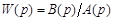 данного устройства:
данного устройства:
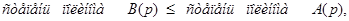 (2)
(2)
то есть старшая производная от входного воздействия по времени не превосходит старшей производной от выходного сигнала по времени.
Применяя преобразование Лапласа к формуле ПИД-регулятора (1), получаем передаточную функцию следующего вида:
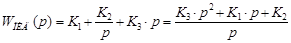 . (3)
. (3)
Очевидно, что степень полинома числителя передаточной функции (3) больше степени полинома знаменателя, то есть условие реализуемости (2) не выполняется. Для того чтобы условие (2) было выполнено, достаточно сделать небольшое допущение – представить передаточную функцию дифференциальной составляющей в следующем виде:
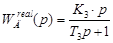 , (4)
, (4)
где коэффициент 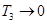 , то есть выбирается как можно меньшим, для того чтобы максимально приблизить дифференциальную составляющую, учитывающую условие реализуемости технического устройства (2) к теоретическому виду (3).
, то есть выбирается как можно меньшим, для того чтобы максимально приблизить дифференциальную составляющую, учитывающую условие реализуемости технического устройства (2) к теоретическому виду (3).
С учетом (4) передаточная функция ПИД-регулятора, удовлетворяющая условию реализуемости технического устройства (2), примет вид:
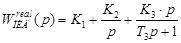 . (5)
. (5)
Согласно структурной схеме (см. рисунок 2) получаем передаточную функцию замкнутой системы и устанавливаем, что если исходное уравнение объекта имеет третий порядок
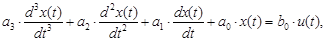 (6)
(6)
то уравнение замкнутой системы имеет пятый порядок, и число оцениваемых параметров увеличивается почти вдвое*:
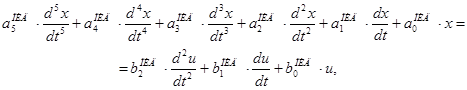 (7)
(7)
что значительно усложняет процесс параметрического моделирования:
________________________
* Рассмотрим вопрос получения дифференциального уравнения замкнутой системы с единичной отрицательной обратной связью при известном дифференциальном уравнении объекта управления. Пусть объект управления описывается уравнением вида (6). Применяя к нему преобразование Лапласа, получим передаточную функцию так называемой неизменяемой части системы.
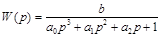 , где
, где 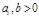 . (7а)
. (7а)
Согласно рисунку 3 с учетом условия реализуемости технического устройства (2) передаточная функция ПИД-регулятора имеет вид (5).
Разомкнутая система (см. рисунок 2) представляет собой последовательное соединение объекта управления и регулятора, а, следовательно, передаточная функция разомкнутой системы имеет вид (в соответствии с правилом преобразования цепей):
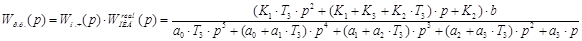 . (7б)
. (7б)
Используя правило Мейсона для замкнутого контура с единичной отрицательной обратной связью:
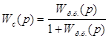 , (7в)
, (7в)
получим передаточную функцию замкнутой системы:
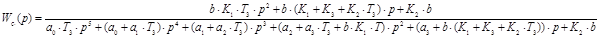 .(7г)
.(7г)
Таким образом, вводя соответствующие обозначения коэффициентов полиномов числителя и знаменателя (7г) и применяя обратное преобразование Лапласа, получаем дифференциальное уравнение замкнутой системы в виде (7).
Чтобы избежать сложности параметрического подхода, предлагается применить для построения модели замкнутой линейной динамической системы непараметрический подход, основанный на оценивании весовой функции системы 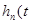 ) (путем предварительного получения непараметрической оценки переходной характеристики замкнутой системы
) (путем предварительного получения непараметрической оценки переходной характеристики замкнутой системы 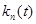 по имеющимся выборочным данным) и для получения динамической непараметрической модели замкнутой ЛДС дальнейшей ее подстановке в интеграл Дюамеля [2]:
по имеющимся выборочным данным) и для получения динамической непараметрической модели замкнутой ЛДС дальнейшей ее подстановке в интеграл Дюамеля [2]:
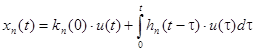 , (8)
, (8)
где в качестве входного сигнала u(t) в силу специфики задачи (макрообъект моделирования – замкнутая система) выступает задающее воздействие 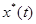 .
.
Оценивание переходной характеристики производится по выборочным данным (поэтому необходима управляемость входного сигнала объекта) как непараметрическая оценка регрессии [3, 4]:
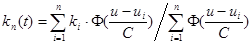 , (9)
, (9)
где n – объем выборочных данных; С – настраиваемый коэффициент непараметрического алгоритма – коэффициент размытости; ki – выборочные измерения переходной характеристики объекта – реакция системы на функцию Хэвисайда [5]:
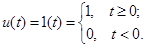 (10)
(10)
Весовая функция, входящая в интеграл Дюамеля (8), находится как производная от переходной характеристики по времени:
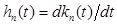 (11)
(11)
и представляет собой реакцию системы на дельта-функцию Дирака, являющуюся производной от функции Хэвисайда по времени. Промежуточное измерение переходной характеристики необходимо потому, что используемая в модели весовая функция вычисляется по этим данным, так как непосредственное измерение весовой функции практически не осуществимо: на вход системы при этом необходимо подавать бесконечно большой сигнал, что в технических устройствах не реализуемо.
Настройка коэффициента размытости C производится из условия минимума среднеквадратичного критерия:
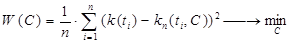 . (12)
. (12)
Приведем результаты построения непараметрической модели для замкнутой системы с единичной отрицательной обратной связью, которую составляют линейный динамический объект, описываемый дифференциальным уравнением третьего порядка (6), и ПИД-регулятор (1).
Первоначально на вход системы необходимо подать единичное ступенчатое воздействие (10). Следует отметить, что для замкнутой системы входным сигналом будет являться задающее воздействие (то есть то, к чему необходимо привести систему), а, следовательно, в качестве переходной характеристики системы при хорошей работе ПИД-регулятора мы должны получить некую кривую, сходящуюся к единице.
По полученным выборочным данным строится непараметрическая оценка переходной характеристики (9), приведенная в сравнении с зашумленными данными выборки на рисунке 4.
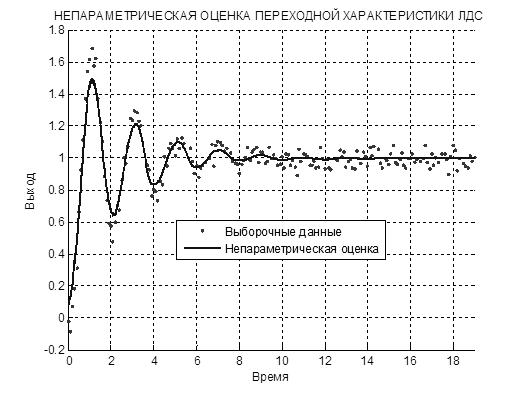
Рис.4 Непараметрическая оценка переходной характеристики системы
На основе (9) получаем оценку весовой функции, которую необходимо сгладить, используя, например, непараметрическую оценку вида (9), и подставить в интеграл Дюамеля (8), где в качестве входного сигнала используется любое воздействие. Полученная непараметрическая модель в сравнении с истинным поведением замкнутой линейной динамической системы с ПИД-регулятором и снятыми выборочными данными (реакция системы на входное задающее воздействие) при задающем синусоидальном воздействии приведены на рисунке 5. Модель достаточно хорошо описывает систему, а неточности могут быть устранены, например, повторной настройкой коэффициента размытости на стадии реакции модели (8) на единичное ступенчатое воздействие, которая как раз будет представлять собой переходную характеристику.
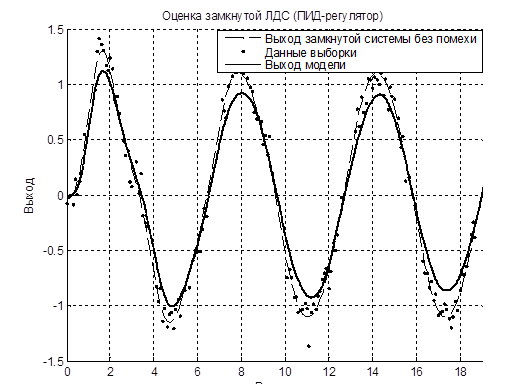
Рис. 5 Результаты построения непараметрической модели замкнутой ЛДС
Таким образом, непараметрический метод, основанный на использовании интеграла Дюамеля, позволяет получать адекватные динамические модели систем при условии, что входной сигнал, поступающий в систему (для замкнутой системы, задающее воздействие), является управляемым. Это требование необходимо для получения используемой в алгоритме оценки весовой функции динамической системы. Наряду с управляемостью требуется наличие информативной выборки, от качества которой напрямую зависит получаемый результат. Отметим также, что данный метод не позволяет получать параметрические модели систем.
Тем не менее, указанный метод достаточно прост в реализации, универсален и, при выполнении условий применимости, позволяет получать непараметрические модели линейных динамических систем разной сложности (не зависимо от типа подключенного параметрического регулятора и порядка дифференциального уравнения объекта). Влияние помех, действующих в каналах измерений, может быть уменьшено, например, выбором при настройке коэффициента размытости критерия, не использующего в явном виде выборочные данные, что повышает степень сглаживания непараметрических оценок и может привести к улучшению модели.
Адекватная модель в свою очередь позволяет перейти к задаче управления замкнутой ЛДС как макрообъектом, повышая при этом качество переходных процессов не путем настройки параметров аналогового регулятора, а путем применения более рациональных методов [1].
Литература
1. Мальцева Т.В. Непараметрическое управление замкнутой ЛДС/ Т.В. Мальцева// Материалы VIII Всероссийской конференции молодых ученых по математическому моделированию и информационным технологиям. – Новосибирск, 2007, с. 59.
2. Медведев А.В. Непараметрические системы адаптации/ А.В.Медведев. – Новосибирск: Наука, 1983. – 176 с.
3. Надарая Э.А. О непараметрических оценках плотности вероятности и регрессии// Теория вероятностей и ее применение. 1965. Т.10(1). С.199-203.
4. Watson G. Smooth regression analysis //Sankhya, ser.A. 1965. Vol.26, part 4. P.~359-372.
5. Юревич Е.И. Теория автоматического управления/ Е.И.Юревич. – СПб: БХВ-Петербург, 2007. – 560с.







